题目内容
设直线l1的方向向量是: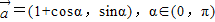 ,直线l2的方向向量为
,直线l2的方向向量为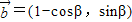 ,β∈(π,2π),直线l3的方向得量是
,β∈(π,2π),直线l3的方向得量是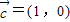 ,l1与l3的夹角为θ1,l2到l3的角为θ2,若
,l1与l3的夹角为θ1,l2到l3的角为θ2,若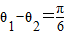 ,试求
,试求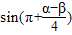 的值.
的值.
【答案】分析:根据直线的方向向量分别求出直线的斜率,再根据到角、夹角公式将 ,转化为α,β的关系,整体代入求解.
,转化为α,β的关系,整体代入求解.
解答:解:由题意得l1的斜率 ,
,
∵l3的方向向量是 ,
,
∴k3=0,
∴l1与l3的夹角为tanθ1= ,又α∈(0,π),
,又α∈(0,π),
∴θ1=
l2的斜率
∴l2到l3的角tanθ2= ,
,
∵β∈(π,2π),
∴θ2=
∵ ,
,
∴ -(
-( )=
)= ,
,
∴ ,
,
∴ =
= =
=
点评:本题考查直线的方向向量的集合意义,直线到角、夹角公式,以及三角函数式的化简求值.
 ,转化为α,β的关系,整体代入求解.
,转化为α,β的关系,整体代入求解.解答:解:由题意得l1的斜率
 ,
,∵l3的方向向量是
 ,
,∴k3=0,
∴l1与l3的夹角为tanθ1=
 ,又α∈(0,π),
,又α∈(0,π),∴θ1=

l2的斜率

∴l2到l3的角tanθ2=
 ,
,∵β∈(π,2π),
∴θ2=

∵
 ,
,∴
 -(
-( )=
)= ,
,∴
 ,
,∴
 =
= =
=
点评:本题考查直线的方向向量的集合意义,直线到角、夹角公式,以及三角函数式的化简求值.

练习册系列答案
相关题目
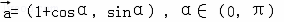 ,直线l2的方向向量为
,直线l2的方向向量为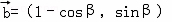 ,β∈(π,2π),直线l3的方向得量是
,β∈(π,2π),直线l3的方向得量是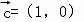 ,l1与l3的夹角为θ1,l2到l3的角为θ2,若
,l1与l3的夹角为θ1,l2到l3的角为θ2,若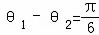 ,试求
,试求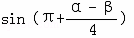 的值.
的值.