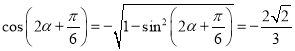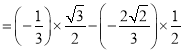Question

【题目】已知四棱锥A-BCDE中,底面BCDE为直角梯形,CD⊥平面ABC,侧面ABCD是等腰直角三角形,∠EBC=∠ABC=90°,BC=CD=2BE,点M是棱AD的中点

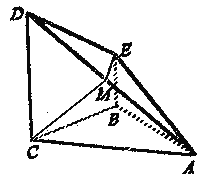
(1)求异面直线ME与AB所成角的大小;

(Ⅱ)证明:平面AED⊥平面ACD

Answer 1

【答案】（1）见解析（2）见解析

【解析】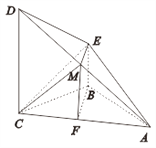

试题分析：（I）取AC的中点F，连接BF，MF. ，证明就是异面直线与所成角，而是等腰直角三角形， ，所以

（II）设法证明平面. 因为，由面面垂直的判定定理即可证得平面.

试题解析：（I）取AC的中点F，连接BF，MF.

因为点是棱的中点，所以.

又因为底面为直角梯形， ，

且，所以.

所以四边形BFME是平行四边形，所以.

所以就是异面直线与所成角，

而是等腰直角三角形， ，所以.

（II）因为，所以.因为平面,所以 .

又所以平面.

所以平面.

而平面，所以平面平面.