题目内容

设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若函数y=f（x）-g（x）在x∈[a，b]上有两个不同的零点，则称f（x）和g（x）在[a，b]上是“关联函数”．若f（x）=x²-3x+4与g（x）=2x+m在[0，3]上是“关联函数”，则m的取值范围为

A.
（-2，4]
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

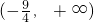
C
分析：根据新定义，将f（x）=x²-3x+4与g（x）=2x+m在[0，3]上是“关联函数”，转化为函数y=x²-5x+4-m在[0，3]上有两个不同的零点即可．
解答：由题意，y=f（x）-g（x）=x²-3x+4-2x-m=x²-5x+4-m，则函数y=x²-5x+4-m在[0，3]上有两个不同的零点，
令h（x）=x²-5x+4-m，则 $\text{[math]}$ ，
∴ $\text{[math]}$ ，解得 $\text{[math]}$
故选C．
点评：本题考查新定义，考查函数零点的研究，解题的关键是理解新定义，将问题进行等价转化．

练习册系列答案

字词句段篇系列答案

自主训练系列答案

自主学习指导课程系列答案

自主创新作业系列答案

认知规律训练法系列答案

钟书金牌期末冲刺100分系列答案

重难点突破训练系列答案

万唯中考预测卷系列答案

初中英语听力课堂系列答案

周测月考单元评价卷系列答案

相关题目

设函数f（x）=a²x²（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为

，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=

，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若对任意x∈[a，b]，都有|f（x）-g（x）|≤1成立，则称f（x）和g（x）在[a，b]上是“紧密函数”．若f（x）=x²-3x+2与g（x）=mx-1在[1，2]上是“紧密函数”，则m的取值范围是（　　）

设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若对任意x∈[a，b]，都有|f（x）-g（x）|≤1成立，则称f（x）和g（x）在[a，b]上是“亲密函数”，区间[a，b]称为“亲密区间”．若f（x）=x²-3x+4与g（x）=2x-1在[a，b]上是“亲密函数”，则b-a的最大值是

设f（x）与g（x）是定义在同一区间[a，b]上的两个函数，若对任意x∈[a，b]，

都有|f（x）-g（x）|≤1成立，则称f（x）和g（x）在[a，b]上是“紧密函数”．若

与g（x）=mx-1在[1，2]上是“紧密函数”，则m的取值范围是（　　）

A．[0，1] B．[2，3] C．[1，2] D．[1，3]

设函数f（x）=a²x²（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2

，求a的值；
（2）关于x的不等式（x-1）²＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=

，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．