题目内容
已知抛物线 过点
过点 .
.
(1)求抛物线 的方程,并求其准线方程;
的方程,并求其准线方程;
(2)过焦点 且斜率为
且斜率为 的直线
的直线 与抛物线交于
与抛物线交于 两点,求
两点,求 的面积.
的面积.
(1)抛物线的方程为 ,准线方程为
,准线方程为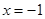 ;(2)
;(2)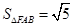 .
.
解析试题分析:(1)先由抛物线 过点
过点 得到
得到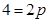 ,进而解出
,进而解出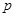 的值,这样即可确定该抛物线的方程,进而再根据抛物线的几何性质得到准线方程
的值,这样即可确定该抛物线的方程,进而再根据抛物线的几何性质得到准线方程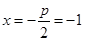 ;(2)由(1)中抛物线的方程先确定
;(2)由(1)中抛物线的方程先确定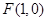 ,进而根据点斜式可写出直线
,进而根据点斜式可写出直线 的方程
的方程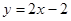 ,设点
,设点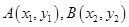 ,联立直线与抛物线的方程,消去
,联立直线与抛物线的方程,消去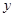 得到
得到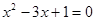 ,进而根据二次方程根与系数的关系得到
,进而根据二次方程根与系数的关系得到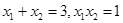 ,进而可根据弦长计算公式
,进而可根据弦长计算公式 计算出弦长
计算出弦长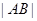 ,然后由点到直线的距离公式算出原点
,然后由点到直线的距离公式算出原点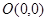 到直线
到直线 的距离
的距离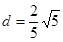 ,进而可求出
,进而可求出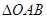 的面积.
的面积.
(1)根据抛物线 过点
过点 可得
可得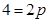 ,解得
,解得
从而抛物线的方程为 ,准线方程为
,准线方程为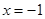 5分
5分
(2)抛物线焦点坐标为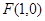 ,所以直线
,所以直线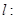
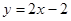 6分
6分
设点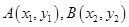
联立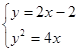 得:
得: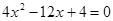 ,即
,即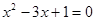 8分
8分
则由韦达定理有: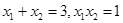 9分
9分
则弦长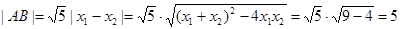 11分
11分
而原点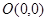 到直线
到直线 的距离
的距离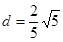 12分
12分
故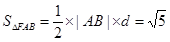 13分.
13分.
考点:1.抛物线的标准方程及其几何性质;2.直线与抛物线的位置关系;3.点到直线的距离公式.

练习册系列答案
相关题目
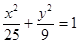 的两个焦点,过F1的直线交椭圆于A、B两点,若
的两个焦点,过F1的直线交椭圆于A、B两点,若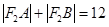 ,则
,则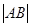 = _____________.
= _____________.  的上焦点为圆心,与该双曲线的渐近线相切的圆的方程为 .
的上焦点为圆心,与该双曲线的渐近线相切的圆的方程为 .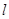 :
: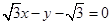 与抛物线
与抛物线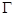 :
: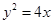 交于
交于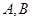 两点,与
两点,与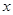 轴交于
轴交于 ,若
,若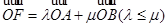 ,则
,则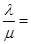 _______.[
_______.[ -
- =1(a·b≠0,且a≠b)与直线x+y-1=0相交于P,Q两点,且
=1(a·b≠0,且a≠b)与直线x+y-1=0相交于P,Q两点,且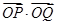 =0(O为原点),则
=0(O为原点),则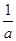 -
- 的值为________.
的值为________.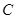 的两个焦点为
的两个焦点为 ,
,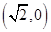 ,一个顶点式
,一个顶点式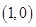 ,则
,则 -
- =1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为____________.
=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为____________. 上任意一点P及点
上任意一点P及点 ,则
,则 的最大值为
的最大值为