题目内容
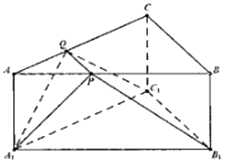
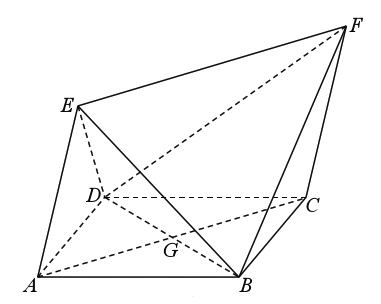
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.
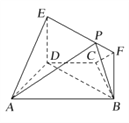
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,试求
,试求![]() 的最小值.
的最小值.
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)利用题意证得![]() .
. ![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,结合题意可得![]()
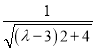 .结合
.结合![]() ,可得
,可得![]() 最大值
最大值![]() ,
, ![]() 的最小值为
的最小值为![]() .
.
试题解析:
(1)证明:在梯形![]() 中,
中,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() .
.
![]() ,
, ![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
![]() 平面
平面![]() ,
, ![]() ,又
,又![]() ,
, ![]() 平面
平面![]() .
.
(2)解:由(1)可建立分别以直线![]() ,
, ![]() ,
, ![]() 为
为![]() 轴,
轴, ![]() 轴,
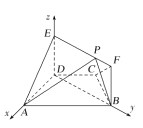
轴, ![]() 轴的空间直角坐标系.如图所示.令
轴的空间直角坐标系.如图所示.令![]() (
(![]() ),则
),则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() 得
得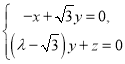
取![]() ,得
,得![]() ,
, ![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
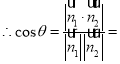
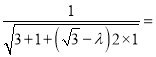
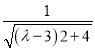 .
.
![]() ,
, ![]() 当
当![]() 时,
时, ![]() 有最大值
有最大值![]() ,
, ![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?