题目内容
已知△ABC中,AB=3,AC=2,D是BC边上一点.A,P,D三点共线,若
=
+
,则△BPD与△CPD的面积比为( )
| AP |
2
| ||
|
|
2
| ||
|
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平面向量的基本定理及其意义
专题:解三角形
分析:利用向量的加法性质可知,AP为∠A的平分线,再利用角平分线的性质
=
=
,即可求得△BPD与△CPD的面积比.
| BD |
| DC |
| AB |
| AC |
| 3 |
| 2 |
解答:
解:△ABC中,设AB方向的单位向量为
,AC方向的单位向量为
,
∵
=
+
=2
+2
,
∴AP为∠A的平分线,
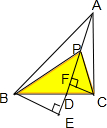
又AB=3,AC=2,D是BC边上一点.A,P,D三点共线,
∴
=
=
,
又△BPD与△CPD的底边均为DP,△BDE∽△CFD,
∴
=
=
,
∴
=
=
=
.
故选:A.
| x1 |
| x2 |
∵
| AP |
2
| ||
|
|
2
| ||
|
|
| x1 |
| x2 |
∴AP为∠A的平分线,

又AB=3,AC=2,D是BC边上一点.A,P,D三点共线,
∴
| BD |
| DC |
| AB |
| AC |
| 3 |
| 2 |
又△BPD与△CPD的底边均为DP,△BDE∽△CFD,
∴
| BD |
| DC |
| BE |
| CF |
| 3 |
| 2 |
∴
| S△BPD |
| S△CPD |
| ||
|
| BD |
| DC |
| 3 |
| 2 |
故选:A.
点评:本题考查平面向量的基本定理及其意义,分析得到AP为∠A的平分线是关键,考查等价转化思想与运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f(x)是定义在R上的奇函数,f(1)=1,当x>0时,有f(x)>xf′(x)恒成立,则不等式f(x)>x的解集是( )
| A、(-1,0)∪(1,+∞) |
| B、(-∞,-1)∪(0,1) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-1,0)∪(0,1) |
函数f(x)=x2,g(x)=log2x,若f(g(x))与g(f(x))的定义域都为[a,b](0<a<b),值域相同,则( )
| A、a≥1,b≤4 |
| B、a=1,b≤1 |
| C、a=1,b=4 |
| D、a≥1,b=4 |
若A,B是相互独立事件,且P(A)=
,P(B)=
,则P(A•
)=( )
| 1 |
| 4 |
| 2 |
| 3 |
. |
| B |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=
,则f(f(0))的值为( )
|
| A、-3 | B、4 | C、5 | D、9 |
数列1,2,2,3,3,3,4,4,4,4,…的第50项是( )
| A、8 | B、9 | C、10 | D、11 |
如图,平行四边形ABCD中,
=(2,0),
=(-3,2),则
•
=( )

| AB |
| AD |
| BD |
| AC |

| A、-6 | B、4 | C、9 | D、13 |