题目内容
3.下列说法中正确的是( )| A. | 命题“若a>b>0,则$\frac{1}{a}$<$\frac{1}{b}$”的逆命题是真命题 | |
| B. | 命题p:?x∈R,x2-x+1>0,则¬p:?x0∈R,x02-x0+1<0 | |
| C. | “a>1,b>1”是“ab>1”成立的充分条件 | |
| D. | “a>b”是“a2>b2”成立的充分不必要条件 |
分析 写出原命题的逆命题,并判断真假,可判断A;写出原命题的否定形式,可判断B;根据充要条件的定义,可判断CD.
解答 解:命题“若a>b>0,则$\frac{1}{a}$<$\frac{1}{b}$”的逆命题是“若$\frac{1}{a}$<$\frac{1}{b}$,则a>b>0”是假命题,故A错误;
命题p:?x∈R,x2-x+1>0,则¬p:?x0∈R,x02-x0+1≤0,故B错误;
当“a>1,b>1”时,“ab>1”成立,故“a>1,b>1”是“ab>1”成立的充分条件,故C正确;
“0>a>b”时,“a2>b2”不成立,故“a>b”不是“a2>b2”成立的充分条件,故D错误,
故选:C
点评 本题考查的知识点是命题的真假判断与应用,四种命题,全(特)称命题,充要条件,难度不大,属于基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
18.已知函数f(x)对任意x,满足f(x)=sinx+2f($\frac{π}{2}$-x),则f($\frac{5π}{4}$)=( )
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
 ,则复数
,则复数 ( )
( ) B.
B. C.
C. D.
D.
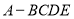 中,底面
中,底面 为矩形,侧面
为矩形,侧面 底面
底面 ,
, ,
, .
.
 ;
; 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值的大小.
的余弦值的大小. ,
, ,则
,则 ( )
( ) B.
B.
 D.
D.
 ,则( )
,则( ) B.
B. C.
C. D.
D.