题目内容
已知圆 ,
,
(Ⅰ)若直线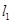 过定点
过定点 (1,0),且与圆
(1,0),且与圆 相切,求
相切,求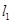 的方程;
的方程;
(Ⅱ) 若圆 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: 上,且与圆
上,且与圆 外切,求圆
外切,求圆 的方程.
的方程.
(Ⅰ)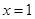 或
或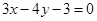 ; (Ⅱ)
; (Ⅱ) 
解析试题分析:(Ⅰ)此问注意直线斜率不存在的情况,应分斜率是否存在进行讨论,当斜率存在时由圆心到直线的距离等于半径求出直线斜率; (Ⅱ)先设出圆心坐标,然后由两圆外切,知圆心距等于两半径之和,从而求出圆心D的坐标,写出圆D方程.
试题解析:(Ⅰ)①若直线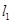 的斜率不存在,即直线是
的斜率不存在,即直线是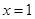 ,符合题意.
,符合题意.
②若直线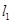 斜率存在,设直线
斜率存在,设直线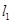 为
为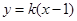 ,即
,即 .
.
由题意知,圆心(3,4)到已知直线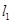 的距离等于半径2,
的距离等于半径2,
即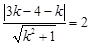 解之得
解之得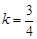 .所求直线方程是
.所求直线方程是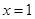 ,
,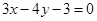 .
.
(Ⅱ)依题意设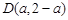 ,又已知圆的圆心
,又已知圆的圆心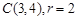 ,
,
由两圆外切,可知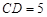
∴可知 =
=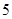 ,解得
,解得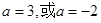 ,∴
,∴ 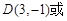
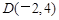 ,
,
∴所求圆的方程为  .
.
考点:1.直线与圆相切;2.两圆相外切;3.点到直线的距离公式.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 的圆与直线
的圆与直线 相切.
相切.
 的标准方程;
的标准方程; ,是否存在定点
,是否存在定点 (不同于原点
(不同于原点 )使得
)使得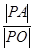 恒为常数?若存在,求出点
恒为常数?若存在,求出点 :
: .
.
 轴相切,求圆
轴相切,求圆 ,圆C与
,圆C与 (点
(点 在点
在点 的左侧).过点
的左侧).过点 :
: 相交于两点
相交于两点 .问:是否存在实数
.问:是否存在实数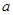 ,使得
,使得 ?若存在,求出实数
?若存在,求出实数 中,点A(0,3),直线
中,点A(0,3),直线 :
: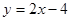 ,设圆
,设圆 的半径为1,圆心在
的半径为1,圆心在
 上,过点A作圆
上,过点A作圆 ,使
,使 ,求圆心
,求圆心 的取值范围.
的取值范围.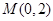 ,
, ,直线
,直线 (
( 为常数).
为常数).  、
、 到直线
到直线 的距离相等,求实数
的距离相等,求实数 ,
,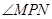 恒为锐角,求实数
恒为锐角,求实数 与直线l:
与直线l: ,且直线l被圆C截得的弦长为
,且直线l被圆C截得的弦长为 .
.  的值;
的值;  时,求过点(3,5)且与圆C相切的直线方程.
时,求过点(3,5)且与圆C相切的直线方程. .请将n表示为m的函数.
.请将n表示为m的函数. 与圆C相切.
与圆C相切. 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B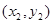 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积. .
. )向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.