题目内容
已知定点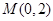 ,
, ,直线
,直线 (
( 为常数).
为常数).
(1)若点 、
、 到直线
到直线 的距离相等,求实数
的距离相等,求实数 的值;
的值;
(2)对于 上任意一点
上任意一点 ,
,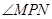 恒为锐角,求实数
恒为锐角,求实数 的取值范围.
的取值范围.
(1) 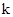 的值为1或
的值为1或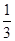 .(2)
.(2)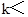
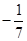 或k>1.
或k>1.
解析试题分析:(1)根据点M,N到直线l的距离相等,可得l∥MN或l过MN的中点.
按l∥MN、l过MN的中点讨论得到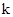 的值为1或
的值为1或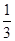 .
.
本题难度不大,但易于出现漏解现象.
(2)根据∠MPN恒为锐角,得知l与以MN为直径的圆相离,即圆心到直线l的距离大于半径,从而建立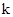 的不等式而得解.
的不等式而得解.
试题解析:(1)∵点M,N到直线l的距离相等,
∴l∥MN或l过MN的中点.
∵M(0,2),N(-2,0),
∴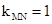 ,MN的中点坐标为C(-1,1).
,MN的中点坐标为C(-1,1).
又∵直线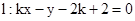 过点D(2,2),
过点D(2,2),
当l∥MN时,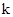 =kMN=1,
=kMN=1,
当l过MN的中点时,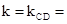
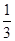 ,
,
综上可知: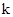 的值为1或
的值为1或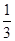 .
.
(2)∵对于l上任意一点P,∠MPN恒为锐角,
∴l与以MN为直径的圆相离,即圆心到直线l的距离大于半径, 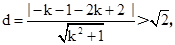
解得: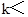
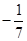 或k>1.
或k>1.
考点:距离,直线与圆的位置关系.

练习册系列答案
相关题目
 经过坐标原点
经过坐标原点 和点
和点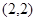 ,且圆心在
,且圆心在 轴上.
轴上.  经过点
经过点 ,且
,且 ,求直线
,求直线 中,已知圆
中,已知圆 :
: 和直线
和直线 :
: ,
, 为
为 ,
, 为圆
为圆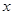 轴的两个交点,直线
轴的两个交点,直线 ,
, 与圆
与圆 .
. 方程;
方程; 外切于点
外切于点 ,且半径为
,且半径为 的圆的方程.
的圆的方程. 与圆
与圆 相交于A、B两点.
相交于A、B两点. 上的圆的方程.
上的圆的方程. ,
,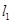 过定点
过定点 (1,0),且与圆
(1,0),且与圆 相切,求
相切,求 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: 上,且与圆
上,且与圆 是圆
是圆 上的点
上的点 的取值范围;
的取值范围; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.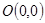 的圆C与直线
的圆C与直线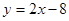 相切于点
相切于点 .
. 的坐标为
的坐标为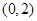 ,设
,设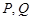 分别是直线
分别是直线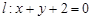 和圆
和圆 上的动点,求
上的动点,求 的最小值.
的最小值. 关于直线
关于直线 对称,且以
对称,且以 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线 、
、 是单位圆
是单位圆 上的点,
上的点, 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形, 且AB∥
为正三角形, 且AB∥
 的三个三角函数值;
的三个三角函数值; 及
及 .
.