Question

已知正四棱柱ABCD-A₁B₁C₁D₁，AB=BC=1，AA₁=2，点E为CC₁的中点，点F为BD₁的中点．
（Ⅰ）证明：EF⊥BD₁；
（Ⅱ）求四面体D₁-BDE的体积．

Answer 1

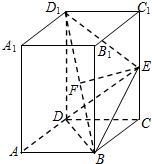
（Ⅰ）证明：∵AB=BC=1，AA₁=2，点E为CC₁中点，
∴EB=

EC2+BC2

=

12+12

=

2

，ED1=

EC12+C1D12

=

12+12

=

2

． …（2分）
∴EB=ED₁．又F为BD₁中点，
∴EF⊥BD₁．                   …（4分）
（Ⅱ）由于VD1-DBE=VB-EDD1，…（6分）
又因为VB-EDD1=

1

3

S△EDD1•BC，而S△EDD1=1，BC=1，
∴VB-EDD1=

1

3

S△EDD1•BC=

1

3

．
故四面体D₁-BDE的体积为

1

3

．                      …（10分）