题目内容
8.已知边长为2的正方形ABCD的四个顶点在球O的球面上,球O的表面积为64π,则四棱锥O-ABCD的体积为$\frac{4\sqrt{14}}{3}$.分析 作平面ABCD的垂线OM,则M为正方形中心,求出OA,AM,OM,然后求解四棱锥O-ABCD的体积.
解答 解:过O作OM⊥平面ABCD,垂足为M,则M为正方形ABCD的中心.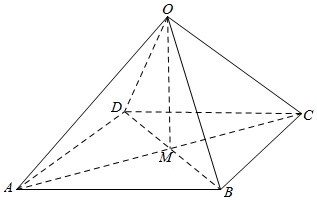
∵正方形ABCD的边长为2,∴AC=2$\sqrt{2}$,AM=$\frac{1}{2}$AC=$\sqrt{2}$,球O的表面积为64π,
∵S球O=4πr2=64π,∴球O的半径OA=r=4.
∴OM=$\sqrt{{4}^{2}-({\sqrt{2})}^{2}}$=$\sqrt{14}$.
则四棱锥O-ABCD的体积为:$\frac{1}{3}×2×2×\sqrt{14}$=$\frac{4\sqrt{14}}{3}$
故答案为:$\frac{4\sqrt{14}}{3}$.
点评 本题考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3.满足z(2+i)=2-i(i为虚数单位)的复数z在复平面内对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.设正项等比数列{an}满足:an•an+1=4n+6,则a100=( )
| A. | 2211 | B. | ($\sqrt{2}$)211 | C. | 4211 | D. | 2105 |
20.设$\overrightarrow{a}$=(x,2),$\overrightarrow{b}$=(x-2,2x),当$\overrightarrow{a}$•$\overrightarrow{b}$最小时,cos<$\overrightarrow{a}$,$\overrightarrow{b}$>的值为( )
| A. | -$\frac{\sqrt{65}}{65}$ | B. | 0 | C. | 1 | D. | -1 |
17.已知定义在R上的函数f(x)=log2(ax-b+1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )

| A. | $0<\frac{1}{a}<\frac{1}{b}<1$ | B. | $0<\frac{1}{b}<a<1$ | C. | $0<b<\frac{1}{a}<1$ | D. | $0<\frac{1}{a}<b<1$ |