题目内容
 已知几何体ABCD-EFG中,ABCD是边长为2的正方形,ADEG与CDEF都是直角梯形,且∠EDA=∠EDC=90°,EF∥CD,EG∥AD,EF∥EG=
已知几何体ABCD-EFG中,ABCD是边长为2的正方形,ADEG与CDEF都是直角梯形,且∠EDA=∠EDC=90°,EF∥CD,EG∥AD,EF∥EG=
(1)求证:AC∥平面BGF;
(2)在AD上求一点M,使GM与平面BFG所成的角的正弦值为
 .
.
【答案】分析:(1)以D点为坐标原点建立的空间坐标系,由已知中ABCD是边长为2的正方形,ADEG与CDEF都是直角梯形,且∠EDA=∠EDC=90°,EF∥CD,EG∥AD,EF∥EG= ,分别求出几何体ABCD-EFG中,各顶点坐标,进而求出直线AC方向向量及平面BGF的法向量,然后判断这两个向量数量积是否为0,即可得到结论.
,分别求出几何体ABCD-EFG中,各顶点坐标,进而求出直线AC方向向量及平面BGF的法向量,然后判断这两个向量数量积是否为0,即可得到结论.
(2)设点M的坐标为(x,0,0),我们分别求出直线GM的方向向量与平面BFG法向量,根据已知GM与平面BFG所成的角的正弦值为 .代入向量夹角公式,构造关于x的方程,解方程,即可确定M点人位置.
.代入向量夹角公式,构造关于x的方程,解方程,即可确定M点人位置.
解答: 证明:(1)∵ED⊥DA,ED⊥DC,ED⊥面ABCD
证明:(1)∵ED⊥DA,ED⊥DC,ED⊥面ABCD
以D点为坐标原点建立如图所示的空间坐标系,
则A(2,0,0),B(2,2,0),C(0,2,0),E(0,0,2),
G(1,0,2),F(0,1,2)…(3分)
 =(-2,2,0),
=(-2,2,0), =(-1,1,0)
=(-1,1,0)
∴ =2
=2 ,即AC∥GF
,即AC∥GF
又∵AC?面BFG,GF?面BFG,AC∥平面BGF…(6分)
(2)设点M的坐标为(x,0,0)
则 =(x-1,0,-2),
=(x-1,0,-2), =(-2,-1,2),
=(-2,-1,2), =(-1,-2,2),
=(-1,-2,2),
设平面BGF的法向量为 ,
,
则可求得 =(1,1,
=(1,1, )…(9分)
)…(9分)
GM与平面BFG所成的角为θ,
则sinθ=|cos< ,
, >|=
>|= =
= 解得x=1,所以M是AD的中点…(12分)
解得x=1,所以M是AD的中点…(12分)
点评:本题考查的知识点是直线与平面平行的判定,直线与平面所成的角,其中建立适当的空间坐标系,将线面关系及夹角问题转化为向量夹角问题是解答此类问题的关键.
 ,分别求出几何体ABCD-EFG中,各顶点坐标,进而求出直线AC方向向量及平面BGF的法向量,然后判断这两个向量数量积是否为0,即可得到结论.
,分别求出几何体ABCD-EFG中,各顶点坐标,进而求出直线AC方向向量及平面BGF的法向量,然后判断这两个向量数量积是否为0,即可得到结论.(2)设点M的坐标为(x,0,0),我们分别求出直线GM的方向向量与平面BFG法向量,根据已知GM与平面BFG所成的角的正弦值为
 .代入向量夹角公式,构造关于x的方程,解方程,即可确定M点人位置.
.代入向量夹角公式,构造关于x的方程,解方程,即可确定M点人位置.解答:
 证明:(1)∵ED⊥DA,ED⊥DC,ED⊥面ABCD
证明:(1)∵ED⊥DA,ED⊥DC,ED⊥面ABCD以D点为坐标原点建立如图所示的空间坐标系,
则A(2,0,0),B(2,2,0),C(0,2,0),E(0,0,2),
G(1,0,2),F(0,1,2)…(3分)
 =(-2,2,0),
=(-2,2,0), =(-1,1,0)
=(-1,1,0)∴
 =2
=2 ,即AC∥GF
,即AC∥GF又∵AC?面BFG,GF?面BFG,AC∥平面BGF…(6分)
(2)设点M的坐标为(x,0,0)
则
 =(x-1,0,-2),
=(x-1,0,-2), =(-2,-1,2),
=(-2,-1,2), =(-1,-2,2),
=(-1,-2,2),设平面BGF的法向量为
 ,
,则可求得
 =(1,1,
=(1,1, )…(9分)
)…(9分)GM与平面BFG所成的角为θ,
则sinθ=|cos<
 ,
, >|=
>|= =
= 解得x=1,所以M是AD的中点…(12分)
解得x=1,所以M是AD的中点…(12分)点评:本题考查的知识点是直线与平面平行的判定,直线与平面所成的角,其中建立适当的空间坐标系,将线面关系及夹角问题转化为向量夹角问题是解答此类问题的关键.

练习册系列答案
相关题目
 已知几何体ABCD-EFG中,ABCD是边长为2的正方形,ADEG与CDEF都是直角梯形,且∠EDA=∠EDC=90°,EF∥CD,EG∥AD,EF∥EG=
已知几何体ABCD-EFG中,ABCD是边长为2的正方形,ADEG与CDEF都是直角梯形,且∠EDA=∠EDC=90°,EF∥CD,EG∥AD,EF∥EG=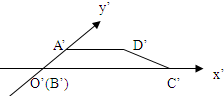 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′如图所示,其中A′D′=2,B′C′=4,A′B′=1,则直角梯形以BC为旋转轴旋转一周形成的几何体的体积为
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′如图所示,其中A′D′=2,B′C′=4,A′B′=1,则直角梯形以BC为旋转轴旋转一周形成的几何体的体积为 DE=1。
DE=1。 。
。 


