题目内容
已知几何体ABCD-EFG中，ABCD是边长为2的正方形，ADEG与CDEF 都是直角梯形，且∠EDA=∠EDC=90°，EF∥CD，EG∥AD，EF=EG=
DE=1。
（1）求证：AC∥平面BGF；
（2）在AD上求一点M，使GM与平面BFG 所成的角的正弦值为
。
DE=1。（1）求证：AC∥平面BGF；
（2）在AD上求一点M，使GM与平面BFG 所成的角的正弦值为
。 
（1）证明： ，ED⊥面ABCD，建立坐标系  ，则  ， ， ，又  面BFG， 面BFG，∴AC∥平面BGF。 （2）解：设点M的坐标为（x，0，0）， 则  ， 设平面BGF的法向量为  ，则可求得 = ，GM与平面BFG所成的角为θ， 则  ，解得x=1，所以M是AD的中点。 |
 |
练习册系列答案
阅读快车系列答案
相关题目
已知几何体ABCD-EFG中，ABCD是边长为2的正方形，ADEG与CDEF都是直角梯形，且∠EDA=∠EDC=90°，EF∥CD，EG∥AD，EF∥EG=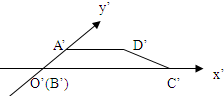
已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′如图所示，其中A′D′=2，B′C′=4，A′B′=1，则直角梯形以BC为旋转轴旋转一周形成的几何体的体积为
已知几何体ABCD-EFG中，ABCD是边长为2的正方形，ADEG与CDEF都是直角梯形，且∠EDA=∠EDC=90°，EF∥CD，EG∥AD，EF∥EG=
．
