题目内容
分别画出函数f(x)=(
)x与g(x)=log
x的简图,并写出f(x)与g(x)的定义域、值域、单调区间.
| 1 |
| 2 |
| 1 |
| 2 |
分析:利用指数函数和对数函数的图象,分别写出函数的定义域,值域和单调区间.
解答: 解:分别作出函数f(x)=(
解:分别作出函数f(x)=(
)x与g(x)=log
x的简图,
则f(x)的定义域为R,值域为(0,+∞),在R上单调递减.
g(x)的定义域为(0,+∞),值域为R,在(0,+∞)上单调递减.
 解:分别作出函数f(x)=(
解:分别作出函数f(x)=(| 1 |
| 2 |
| 1 |
| 2 |
则f(x)的定义域为R,值域为(0,+∞),在R上单调递减.
g(x)的定义域为(0,+∞),值域为R,在(0,+∞)上单调递减.
点评:本题主要考查指数函数和对数函数的图象和性质,比较基础.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

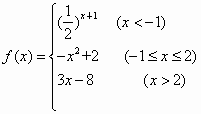 .
.
 +b2(a1,a2,b2∈R).
+b2(a1,a2,b2∈R).