题目内容
设函数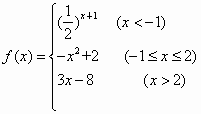 .
.
(Ⅰ)请在下列直角坐标系中画出函数f(x)的图象;
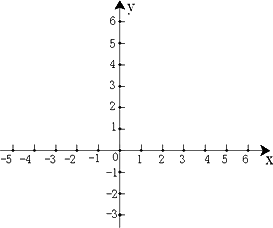
(Ⅱ)根据(Ⅰ)的图象,试分别写出关于x的方程f(x)=t有2,3,4个实数解时,相应的实数t的取值范围;
(Ⅲ)记函数g(x)的定义域为D,若存在x0∈D,使g(x0)=x0成立,则称点(x0,x0)为函数g(x)图象上的不动点.试问,函数f(x)图象上是否存在不动点,若存在,求出不动点的坐标,若不存在,请说明理由.
答案:
解析:
解析:
|
解:(Ⅰ)函数
(Ⅱ)根据图象可知 当 当 当 (Ⅲ)若 由图象可知: 若 若 综上,函数 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

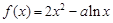
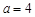 ,求函数
,求函数 的极小值;
的极小值;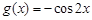 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量 使得
使得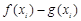 的值相等,若存在,请求出
的值相等,若存在,请求出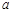 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?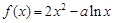
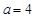 ,求函数
,求函数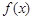 的极小值;
的极小值;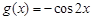 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量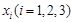
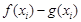 的值相等,若存在,请求出
的值相等,若存在,请求出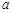 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?