题目内容
设
为两两不重合的平面，
为两两不重合的直线，给出下列四个命题：
（1）若
，则
；
（2）若
,
，
，则；
（3）若，
，则
；
（4）若
，
，
，
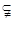
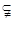
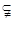
，则
．
其中正确的命题是（ ）
| A．（1）（3） | B．（2）（3） |
| C．（2）（4） | D．（3）（4） |
D
解析试题分析：（1）不正确，面
可能相交。（2）不正确，当直线
平行时，还可能相交；根据面面平行的判定定理只有当相交时，。（3）正确，根据面面平行定义可知与
无公共点，即可知。（4）正确，因为，可知
，又因为，，则。综上可得D正确。
考点：1线面位置关系、面面位置关系；2线面平行、面面平行的判定；3线面平行的性质定理。
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
在正方体
中，与
所在直线所成的角为
是（ ）
A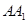． | B． | C． | D． |
若直线l不平行于平面α,且l?α,则( )
| A．α内的所有直线与l异面 |
| B．α内不存在与l平行的直线 |
| C．α内存在唯一的直线与l平行 |
| D．α内的直线与l都相交 |
设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列命题,其中正确的命题是( )
①P∈a,P∈α⇒a?α;
②a∩b=P,b?β⇒a?β;
③a∥b,a?α,P∈b,P∈α⇒b?α;
④α∩β=b,P∈α,P∈β⇒P∈b.
| A．①② | B．②③ | C．①④ | D．③④ |
设l为直线，α，β 是两个不同的平面，下列命题中正确的是
( )．
| A．若l∥α，l∥β，则α∥β | B．若l⊥α，l⊥β，则α∥β |
| C．若l⊥α，l∥β，则α∥β | D．若α⊥β，l∥α，则l⊥β |
如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是( )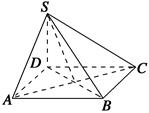 
| A．AC⊥SB |
| B．AB∥平面SCD |
| C．SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D．AB与SC所成的角等于DC与SA所成的角 |
在正四面体P－ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的( )．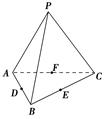
| A．BC∥平面PDF | B．DF⊥平面PAE |
| C．平面PDF⊥平面ABC | D．平面PAE⊥平面ABC |
设a，b为两条直线，α，β为两个平面，则下列结论成立的是( )．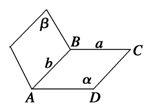
| A．若a?α，b?β，且α∩β＝l，则a∥b |
| B．若a?α，b?β，且a⊥b，则α⊥β |
| C．若a∥α，b?α，则a∥b |
| D．若a⊥α，b⊥α，则a∥b |