题目内容
已知函数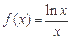 .
.
(1)求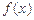 在点
在点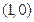 处的切线方程;
处的切线方程;
(2)求函数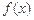 在
在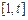 上的最大值.
上的最大值.
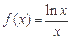 .
.(1)求
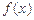 在点
在点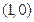 处的切线方程;
处的切线方程;(2)求函数
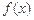 在
在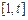 上的最大值.
上的最大值. 的定义域为
的定义域为 ,
, 的导数
的导数 .
. (Ⅰ)
 ,所以切线方程为:
,所以切线方程为: .
.(Ⅱ)令
 ,解得
,解得
当
 时,
时, ,
, 单调递增,当
单调递增,当 时,
时, ,
, 单调递减.
单调递减.当
 时,
时, 在
在 上单调递增,
上单调递增,
当
 时,
时, 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,

略

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
题目内容
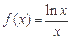 .
.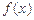 在点
在点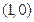 处的切线方程;
处的切线方程;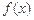 在
在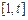 上的最大值.
上的最大值. 的定义域为
的定义域为 ,
, 的导数
的导数 .
.  ,所以切线方程为:
,所以切线方程为: .
. ,解得
,解得
 时,
时, ,
, 单调递增,当
单调递增,当 时,
时, ,
, 单调递减.
单调递减. 时,
时, 在
在 上单调递增,
上单调递增,
 时,
时, 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案