题目内容
一个均匀的正四面体的四个面上分别标有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为x1,x2,记ξ=(x1-3)2+(x2-3)2.
(1)分别求出ξ取得最大值和最小值时的概率.
(2)求ξ的分布列.
解 (1)掷出点数x可能是1,2,3,4,则x-3分别得:-2,-1,0,1.于是(x-3)2的所有取值分别为:0,1,4.因此ξ的所有取值为:0,1,2,4,5,8.
当x1=1且x2=1时,ξ=(x1-3)2+(x2-3)2可取得最大值8,
P(ξ=8)= ×
× =
= ;
;
当x1=3且x2=3时,ξ=(x1-3)2+(x2-3)2可取得最小值0,
P(ξ=0)= ×
× =
= .
.
所以ξ取得最大值和最小值时的概率均为 .
.
(2)由(1)知ξ的所有取值为:0,1,2,4,5,8.
P(ξ=0)=P(ξ=8)= ;
;
当ξ=1时,(x1,x2)的所有取值为(2,3),(4,3),(3,2),(3,4).
即P(ξ=1)= =
= ;
;
当ξ=2时,(x1,x2)的所有取值为(2,2),(4,4),(4,2),(2,4).
即P(ξ=2)= =
= ;
;
当ξ=4时,(x1,x2)的所有取值为(1,3),(3,1).
即P(ξ=4)= =
= ;
;
当ξ=5时,(x1,x2)的所有取值为(2,1),(1,4),(1,2),(4,1).
即P(ξ=5)= =
= .
.
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 4 | 5 | 8 |
| P |
|
|
|
|
|
|

某射手射击所得环数X的分布列为:
| X | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 0.02 | 0.04 | 0.06 | 0.09 | 0.28 | 0.29 | 0.22 |
则此射手“射击一次命中环数大于7”的概率为( )
A.0.28 B.0.88
C.0.79 D.0.51
为了参加2014年青奥会高中篮球比赛,某中学决定从四个篮球较强的班级中选出12人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
| 班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
| 人数 | 4 | 2 | 3 | 3 |
(1)从这12名队员中随机选出两名,求两人来自同一班级的概率;
(2)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为ξ,求随机变量ξ的分布列.
 B.16π C.9π D.
B.16π C.9π D.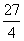
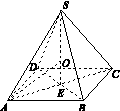
 ﹣x2=1,点A的坐标为(0,﹣
﹣x2=1,点A的坐标为(0,﹣ ),B是圆(x﹣
),B是圆(x﹣ 若f(2m-1)<
若f(2m-1)< ,则m的取值范围是( )
,则m的取值范围是( )