题目内容
若向量a、b、c满足a+b+c=0,|a|=3,|b|=1,|c|=4,则a•b+b•c+c•a等于
- A.-11
- B.-12
- C.-13
- D.-14
C
分析:把本题所给的三个向量的和两边平方,得到右边为零,左边是包含要求的三个向量两两求数量积的式子,把已知的三个向量的模代入,得到要求的结果.
解答:∵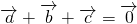 ,
,
∴( )(
)( )=0
)=0
∴ +
+ +
+ +2
+2 =0
=0
∵| |=3,|
|=3,| |=1,|
|=1,| |=4
|=4
∴ +
+ +2
+2 =0-9-1-16=-26,
=0-9-1-16=-26,
∴ +
+ +
+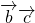 =-13,
=-13,
故选C.
点评:本题是一个考查数量积的应用问题,在解题时注意启发学生在理解数量积的运算特点的基础上,把握数量积的运算律,注意数量积性质的相关问题的特点.
分析:把本题所给的三个向量的和两边平方,得到右边为零,左边是包含要求的三个向量两两求数量积的式子,把已知的三个向量的模代入,得到要求的结果.
解答:∵
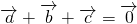 ,
,∴(
 )(
)( )=0
)=0∴
 +
+ +
+ +2
+2 =0
=0∵|
 |=3,|
|=3,| |=1,|
|=1,| |=4
|=4∴
 +
+ +2
+2 =0-9-1-16=-26,
=0-9-1-16=-26,∴
 +
+ +
+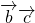 =-13,
=-13,故选C.
点评:本题是一个考查数量积的应用问题,在解题时注意启发学生在理解数量积的运算特点的基础上,把握数量积的运算律,注意数量积性质的相关问题的特点.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
若向量
,
,
满足
∥
且
⊥
,则
•(
+2
)=( )
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| c |
| a |
| b |
| A、4 | B、3 | C、2 | D、0 |