题目内容
若函数y=loga(x2﹣ax+1)有最小值,则a的取值范围是( )
| A.0<a<1 | B.0<a<2,a≠1 | C.1<a<2 | D.a≥2 |
C
解析试题分析:令 ,则
,则 ,当0<a<1时,
,当0<a<1时, 为减函数,而
为减函数,而 的
的 ,因此原函数定义域为R,在
,因此原函数定义域为R,在 上增,
上增, 上减无最小值;当a≥2时,
上减无最小值;当a≥2时, 为增函数,而
为增函数,而 的
的 ,原函数的定义域为两开区间,且在这两个区间上具有单调性,无最值,排除了A、B、D,答案选C.
,原函数的定义域为两开区间,且在这两个区间上具有单调性,无最值,排除了A、B、D,答案选C.
考点:1.对数函数的单调性;2.二次函数的单调性;3.复合函数的单调性与最值

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知函数 则
则 的值为( )
的值为( )
A. | B.4 | C.2 | D. |
设 ,函数
,函数 在区间
在区间 上的最大值与最小值之差为
上的最大值与最小值之差为 ,则
,则 ( )
( )
A. | B.2 | C. | D.4 |
“因为对数函数 是增函数,而
是增函数,而 是对数函数,所以
是对数函数,所以 是增函数”.这个推理是错误的,是因为( )
是增函数”.这个推理是错误的,是因为( )
| A.推理形式错误 | B.小前提错误 | C.大前提错误 | D.非以上错误 |

 为奇函数,当
为奇函数,当 时,
时,  的最小值为2.
的最小值为2. ,求证:
,求证:


 且
且 ,求证:
,求证:
 函数
函数 .
. 的奇偶性,并求其最大值;
的奇偶性,并求其最大值; ;
; 的图象
的图象 与
与 轴所围成的图形的面积不小于
轴所围成的图形的面积不小于 .
.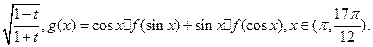
 ________.
________.