题目内容
(本小题满分12分) 函数
函数 .
.
(Ⅰ) 判断函数 的奇偶性,并求其最大值;
的奇偶性,并求其最大值;
(Ⅱ) 求证: ;
;
(Ⅲ) 求证: 的图象
的图象 与
与 轴所围成的图形的面积不小于
轴所围成的图形的面积不小于 .
.
(Ⅰ)偶函数,最大值
(Ⅱ)证明见解析
(Ⅲ)证明见解析
解析(Ⅰ)定义域为 ,
, ,则
,则 为偶函数,
为偶函数, ,则
,则 ,
,
所以函数 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
则最大值 ;------------------------------------------------------
;------------------------------------------------------ 4分
4分
(Ⅱ)要证明 ,
,
只 需证
需证 ,
,
设
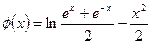 ,
,
则
令
 ,则
,则
所以, 在
在 上为单调递减函数,
上为单调递减函数,
因此,
所以当 时,
时,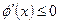 ,又因为
,又因为 ,则
,则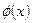 为偶函数,
为偶函数,
所以 ,则原结论成立;-
,则原结论成立;- ---------------------------------------8分
---------------------------------------8分
(Ⅲ)由标准正态分布 与
与 轴围成的面积为
轴围成的面积为 ,
,
则由(Ⅱ)得 ,
,
则 ,
,
所以 的图象与
的图象与 轴所围成的图形的面积不小于
轴所围成的图形的面积不小于 .------------------12分
.------------------12分

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
若函数y=loga(x2﹣ax+1)有最小值,则a的取值范围是( )
| A.0<a<1 | B.0<a<2,a≠1 | C.1<a<2 | D.a≥2 |
设a=40.9,b=80.48, ,则( ).
,则( ).
| A.c>a>b | B.b>a>c | C.a>b>c | D.a>c>b |
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,
 上的单调性,并用单调性的定义证明;
上的单调性,并用单调性的定义证明; 的值域.
的值域. ,
,
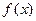 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,是否存在实数
,是否存在实数
 (
( 是自然常数)时,函数
是自然常数)时,函数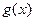 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的定义域为
的定义域为 ,对任意实数
,对任意实数 ,都有
,都有 成立,且当
成立,且当 时,有
时,有 ,试判断函数
,试判断函数 为定义在R上的奇函数,且当
为定义在R上的奇函数,且当 时,
时, ,
,
 时
时 的方程
的方程 有解,求实数
有解,求实数 的范围。
的范围。 的最大和最小值.
的最大和最小值. ,函数
,函数 (
( ,求函数
,求函数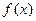 的最小值.
的最小值.