Question

已知函数，，，满足：

         ① 对任意，，，都有；

         ② 对任意都有．

   （Ⅰ）试证明：为上的单调增函数；

   （Ⅱ）求；

   （Ⅲ）令，，试证明：

Answer 1

（Ⅱ）66

解析:

（I）由①知，对任意，都有，

由于，从而，所以函数为上的单调增函数.  

（II）令，则，显然，否则，与矛盾.从而，而由,即得.

又由（I）知，即.

于是得，又，从而，即.                

进而由知，.

于是,                                     

,

,

,

,

,

由于,

而且由（I）知，函数为单调增函数，因此.

从而.                          

（III）,

，.

即数列是以6为首项, 以3为公比的等比数列 .

 ∴ .                             

于是,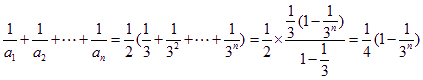

显然,                                              

综上所述,