题目内容
(本题满分16分)
已知 ,函数
,函数 .
.
(1) 如果实数 满足
满足 ,函数
,函数 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的
值,如果没有,说明为什么?
(2) 如果 判断函数
判断函数 的单调性;
的单调性;
(3) 如果 ,
, ,且
,且 ,求函数
,求函数 的对称轴或对称中心.
的对称轴或对称中心.
【答案】
.(16分)

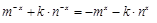 恒成立,(4分)
恒成立,(4分)
即: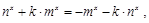
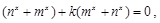 (5分)
(5分)
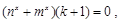 由
由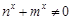 恒成立,得
恒成立,得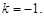 (6分)
(6分)
(2)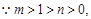
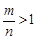 ,
,
∴ 当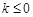 时,显然
时,显然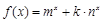 在R上为增函数;(8分)
在R上为增函数;(8分)
当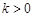 时,
时,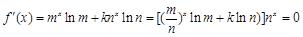 ,
,
由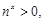 得
得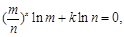 得
得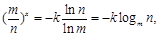
得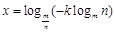 .(9分)
.(9分)
∴当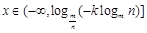 时,
时, 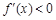 ,
,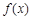 为减函数; (10分)
为减函数; (10分)
当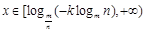 时,
时, 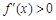 ,
,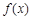 为增函数. (11分)
为增函数. (11分)
(3) 当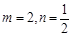 时,
时,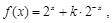
如果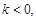
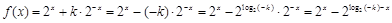 ,(13分)
,(13分)
则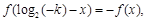
∴函数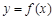 有对称中心
有对称中心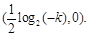 (14分)
(14分)
如果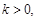
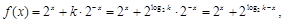 (15分)
(15分)
则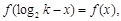
∴函数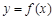 有对称轴
有对称轴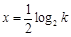 .(16分)
.(16分)
【解析】略

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在