Question

【题目】平面上有12个点且任意三点不共线.以其中任意一点为始点、另一点为终点作向量且作出所有的向量，其中，三边向量的和为零向量的三角形称为“零三角形”.求以这12个点为顶点的零三角形个数的最大值.

Answer 1

【答案】70

【解析】

设这12个点分别为.这12个点确定的三角形共有个，设以为始点的向量数为.

若以某三点为顶点的三角形为非零三角形，则有且仅有一个点是此三角形两边向量的始点，所以，以为顶点之一且为两边始点的非零三角形有个.从而，以这些点为顶点的三角形中非零三角形的总数为.

因此，零三角形的个数为.

先求的最小值.

因为，所以，.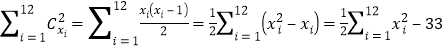

而非负整数不超过11，故有最小值.

由调整法知，当，即当时，取最小值366.

故的最小值为.

因此，以这12个点为顶点的零三角形个数的最大值为70.