题目内容
 如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形.
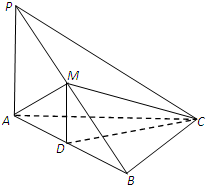
如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形.(1)求证:BC⊥平面PAC;
(2)若BC=4,PB=10,求四棱锥C-ADMP的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)要证BC⊥平面PAC,只需证明BC与平面PAC内的两条相交直线PA、PC垂直,利用直线与平面垂直的判定定理证明即可;
(2)利用四棱锥C-ADMP的体积=VP-ABC-VM-BCD,即可求得结论.
(2)利用四棱锥C-ADMP的体积=VP-ABC-VM-BCD,即可求得结论.
解答:
 (1)证明:在正△AMB中,D是AB的中点,∴MD⊥AB.
(1)证明:在正△AMB中,D是AB的中点,∴MD⊥AB.
∵M是PB的中点,D是AB的中点,∴MD∥PA,故PA⊥AB.
又PA⊥AC,AB∩AC=A,AB,AC?平面ABC,
∴PA⊥平面ABC.
∵BC?平面ABC,∴PA⊥BC,
又PC⊥BC,PA∩PC=P,PA,PC?平面PAC,
∴BC⊥平面PAC.…(8分)
(2)解:∵△AMB为正三角形,∴AB=MB=5.…(9分)
∵BC=4,BC⊥AC,∴AC=3.
∵PB=10,M是PB的中点,∴MB=5.
∵△AMB为正三角形,∴AB=MB=5.…8分
∵BC=4,BC⊥AC,∴AC=3.
∴S△BCD=
S△ABC=
×
×3×4=3.…9分
∵MD=
=
,
由(1)知MD∥PA,∴MD⊥DC.
在△ABC中,CD=
AB=
,
∴S△MCD=
×
×
=
.…10分
∴VM-BCD=VB-MCD=
×3×
=
,
在Rt△PCB中,PC=
=
,PA=2MD=5
故VP-ABC=
×
×AC×BC×PA=
×
×3×4×5
=10
∴四棱锥C-ADMP的体积=VP-ABC-VM-BCD=10
-
=
…12分.
 (1)证明:在正△AMB中,D是AB的中点,∴MD⊥AB.
(1)证明:在正△AMB中,D是AB的中点,∴MD⊥AB.∵M是PB的中点,D是AB的中点,∴MD∥PA,故PA⊥AB.
又PA⊥AC,AB∩AC=A,AB,AC?平面ABC,
∴PA⊥平面ABC.
∵BC?平面ABC,∴PA⊥BC,
又PC⊥BC,PA∩PC=P,PA,PC?平面PAC,
∴BC⊥平面PAC.…(8分)
(2)解:∵△AMB为正三角形,∴AB=MB=5.…(9分)
∵BC=4,BC⊥AC,∴AC=3.
∵PB=10,M是PB的中点,∴MB=5.
∵△AMB为正三角形,∴AB=MB=5.…8分
∵BC=4,BC⊥AC,∴AC=3.
∴S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵MD=
52-(
|
5
| ||
| 2 |
由(1)知MD∥PA,∴MD⊥DC.
在△ABC中,CD=
| 1 |
| 2 |
| 5 |
| 2 |
∴S△MCD=
| 1 |
| 2 |
5
| ||
| 2 |
| 5 |
| 2 |
25
| ||
| 8 |
∴VM-BCD=VB-MCD=
| 1 |
| 3 |
5
| ||
| 2 |
5
| ||
| 2 |
在Rt△PCB中,PC=
| PB2-BC2 |
| 84 |
| 3 |
故VP-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∴四棱锥C-ADMP的体积=VP-ABC-VM-BCD=10
| 3 |
5
| ||
| 2 |
15
| ||
| 2 |
点评:本题考查直线与平面垂直的判断与证明,考查四棱锥的体积,考查空间想象能力以及逻辑推理能力,属于中档题.

练习册系列答案
相关题目
已知向量
与向量
的夹角为60°,且|
|=1,|
|=2,若
=
+λ
,
⊥(2
-
),则实数λ的值为( )
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
A、λ=
| ||
B、λ=
| ||
C、λ=
| ||
| D、λ=1 |
已知F是抛物线y2=4x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
A、
| ||
| B、1 | ||
C、
| ||
D、
|
已知f(x)=log2(x-2),若实数m,n满足f(m)+f(2n)=3,则m+n的最小值是( )
| A、7 | B、5 | C、3 | D、4 |
 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.