题目内容
已知函数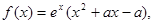 其中
其中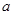 是常数.
是常数.
(1)当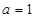 时,求
时,求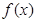 在点
在点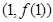 处的切线方程;
处的切线方程;
(2)求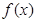 在区间
在区间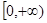 上的最小值.
上的最小值.
【答案】
解:(1)由 可得
可得
 .
.
当 时,
时, ,
, .
.
所以 曲线 在点
在点 处的切线方程为
处的切线方程为 ,
,
即 . -----------(7分)
. -----------(7分)
(2)令 ,解得
,解得 或
或 .
.
当 ,即
,即 时,在区间
时,在区间 上,
上, ,所以
,所以 是
是 上的增函数.
上的增函数.
所以 的最小值为
的最小值为 =
= ; ----------(10分)
; ----------(10分)
当 ,即
,即 时,
时,  随
随 的变化情况如下表
的变化情况如下表
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↘ |
|
↗ |
由上表可知函数 的最小值为
的最小值为 .-------(15分)
.-------(15分)
【解析】略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目








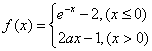 (
(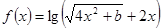 ,其中
,其中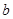 是常数.
是常数.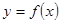 是奇函数,求
是奇函数,求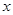 轴.
轴.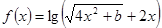 ,其中
,其中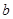 是常数.
是常数.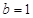 时,
时,
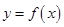 是奇函数;
是奇函数;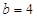 时,
时,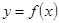 的图像上不存在两点
的图像上不存在两点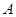 、
、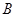 ,使得直线
,使得直线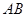 平行于
平行于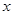 轴.
轴.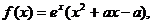 其中
其中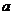 是常数.
是常数.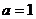 时,求
时,求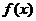 在点
在点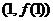 处的切线方程;
处的切线方程;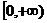 上的最小值.
上的最小值.