题目内容
某餐厅有 四个桌子,每个桌子最多坐8人,现有11人进入餐厅,随意的坐下吃饭,已知
四个桌子,每个桌子最多坐8人,现有11人进入餐厅,随意的坐下吃饭,已知 桌一定有人坐,其他桌子可能有人坐,也可能没人坐,则四个桌子坐的人数的不同的情况有多少种( )
桌一定有人坐,其他桌子可能有人坐,也可能没人坐,则四个桌子坐的人数的不同的情况有多少种( )
| A.286 | B.276 | C.264 | D.246 |
C
解析试题分析:因为, 桌一定有人坐,所以,分类讨论如下。A桌分别坐1,2,3,……8人,其他人坐B,C,D桌,利用“挡板法”。将余下的10人分三堆时,不能有超过8人的,有
桌一定有人坐,所以,分类讨论如下。A桌分别坐1,2,3,……8人,其他人坐B,C,D桌,利用“挡板法”。将余下的10人分三堆时,不能有超过8人的,有 种方法,9人,……3人,分三堆,方法数为
种方法,9人,……3人,分三堆,方法数为 197
197
考点:组合数公式的应用
点评:简单题,注意理解四个桌子坐的人数的不同的情况,将10,9,8,……3人分成三堆。

练习册系列答案
相关题目
某教师一天上3个班级的课,每班一节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5和第6节不算连上),那么这位教师一天的课的所有排法有( )
| A.474种 | B.77种 | C.462种 | D.79种 |
将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两个端点异色,若只有5种颜色可供使用,则不同的染色方法总数有 ( )
| A. 240种 | B. 300种 | C.360种 | D.420种 |
设m∈N*,且m<45,则(45-m)(46-m)(47-m)……(60-m),用排列数符号表示为( )
| A.A60-m15 | B.A60-m16 | C.A60-m45-m | D.A45-m16 |
如果 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中 的系数是 ( )
的系数是 ( )
| A.-2835 | B.2835 | C.21 | D.-21 |
4名学生被人大、清华、北大录取,若每所大学至少要录取1名,则共有不同的录取方法( )
| A.72种 | B.36种 | C.24种 | D.12种 |
已知(1+ x)(1+x)5的展开式中x2的系数为5,则
x)(1+x)5的展开式中x2的系数为5,则 =
=
| A.-4 | B.-3 | C.-2 | D.-1 |
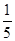



 个座位,现有
个座位,现有 名观众就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,那么不同的坐法种数共有 ( )
名观众就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,那么不同的坐法种数共有 ( ) 


