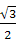题目内容
在三角形ABC中,bcosC=ccosB,则三角形ABC是
等腰
等腰
三角形.分析:运用正弦定理,化简ccosB=bcosC,即sinCcosB=sinBcosC⇒sin(B-C)=0,B=C,推出三角形的形状.
解答:解:∵bcosC=ccosB
∴sinCcosB=sinBcosC
∴sin(B-C)=0
∴B=C
∴三角形是等腰三角形.
故答案为:等腰.
∴sinCcosB=sinBcosC
∴sin(B-C)=0
∴B=C
∴三角形是等腰三角形.
故答案为:等腰.
点评:本题考查正弦定理的应用,三角形形状的判断,基本知识的有考查.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
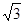 , 则AB+2BC的最大值为( )
, 则AB+2BC的最大值为( )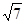 D.
2
D.
2 ,C=60
,C=60 B.
B.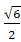 C.
C. D.
D.