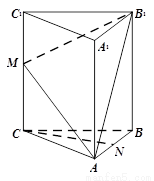
题目内容
(本小题共14分)如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为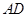 的中点,
的中点,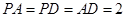 .
.
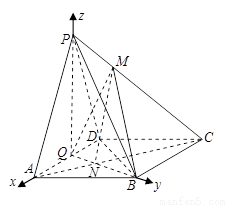
(Ⅰ)求证: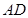
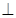 平面
平面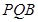 ;
;
(Ⅱ)点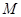 在线段
在线段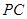 上,
上,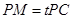 ,试确定
,试确定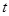 的值,使
的值,使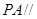 平面
平面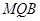 ;
;
(Ⅲ)若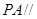 平面
平面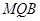 ,平面
,平面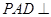 平面
平面 ,求二面角
,求二面角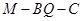 的大小.
的大小.
证明:(Ⅰ)连接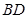 .
.
因为四边形 为菱形,
为菱形,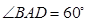 ,
,
所以△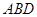 为正三角形.又
为正三角形.又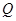 为
为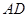 中点,
中点,
所以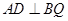 .
.
因为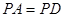 ,
,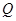 为
为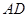 的中点,
的中点,
所以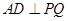 .
.
又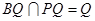 ,
,
所以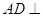 平面
平面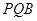 .
………………4分
.
………………4分
(Ⅱ)当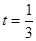 时,
时,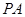 ∥平面
∥平面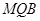 .
.
下面证明:
连接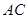 交
交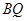 于
于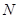 ,连接
,连接 .
.

因为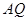 ∥
∥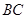 ,
,
所以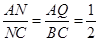 .
.
因为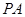 ∥平面
∥平面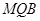 ,
,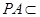 平面
平面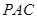 ,平面
,平面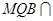 平面
平面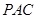
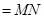 ,
,
所以 ∥
∥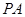 .
.
所以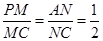 .
.
所以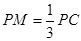 ,即
,即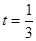 .
.
因为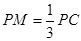 ,
,
所以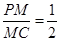 .
.
所以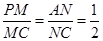 ,
,
所以 ∥
∥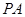 .
.
又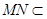 平面
平面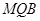 ,
,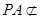 平面
平面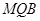 ,
,
所以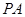 ∥平面
∥平面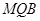 .
…………9分
.
…………9分
(Ⅲ)因为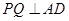 ,
,
又平面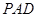
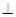 平面
平面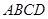 ,交线为
,交线为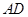 ,
,
所以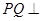 平面
平面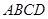 .
.
以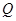 为坐标原点,分别以
为坐标原点,分别以 所在的直线为
所在的直线为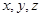 轴,建立如图所示的空间直
轴,建立如图所示的空间直
角坐标系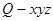 .
.
由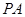 =
= =
=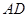 =2,
=2,
则有 ,
,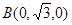 ,
,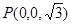 .
.
设平面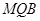 的法向量为
的法向量为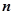 =
=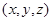 ,
,
由 ,
,
且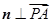 ,
,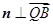 ,
,
可得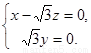
令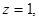 得
得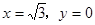 .
.
所以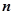 =
=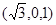 为平面
为平面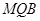 的一个法向量.
的一个法向量.
取平面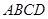 的法向量
的法向量 =
=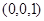 ,
,
则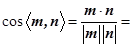
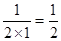 ,
,
故二面角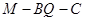 的大小为60°.
…………14分
的大小为60°.
…………14分
【解析】本题考查线面垂直和二面角、探索性问题等综合问题。考查学生的空间想象能力。线面垂直的证明方法:(1)线面垂直的定义;(2)线面垂直的判断定理;(3)面面垂直的性质定理;(4)向量法:证明这个直线的方向向量和这个平面的法向量相互平行.
线面垂直的证明思考途径:线线垂直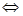 线面垂直
线面垂直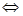 面面垂直.本题第一问利用方法二进行证明;探求某些点的具体位置,使得线面满足垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.本题第二问主要采用假设存在点,然后确定线面平行的性质进行求解. 本题第三问利用向量法求解二面角.
面面垂直.本题第一问利用方法二进行证明;探求某些点的具体位置,使得线面满足垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.本题第二问主要采用假设存在点,然后确定线面平行的性质进行求解. 本题第三问利用向量法求解二面角.

 阅读快车系列答案
阅读快车系列答案

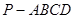 中,底面
中,底面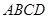 为平行四边形,
为平行四边形,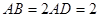 ,
,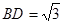 ,
, ⊥底面
⊥底面
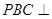 平面
平面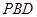 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。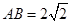 ,CC1=4,M是棱CC1上一点.
,CC1=4,M是棱CC1上一点.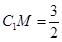 ,求二面角A-MB1-C的大小.
,求二面角A-MB1-C的大小.