题目内容
如图,矩形纸板ABCD的顶点A、B分别在正方形边框EOFG的边OE、OF上,当点B在OF边上进行左右运动时,点A随之在OE上进行上下运动.若AB=8,BC=3,运动过程中,则点D到点O距离的最大值为


A. | B.9 | C.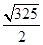 | D.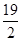 |
B
试题分析:因为
 是直角三角形,所以不论A,B怎样移动,点O始终在
是直角三角形,所以不论A,B怎样移动,点O始终在 的外接圆上,
的外接圆上, 的中点为外接圆的圆心,所以当点O,D和
的中点为外接圆的圆心,所以当点O,D和 的中点共线时,点D到点O距离最大,此时最大距离为
的中点共线时,点D到点O距离最大,此时最大距离为
点评:解决本小题的关键是找出当点O,D和
 的中点共线时,点D到点O距离最大,解决此类问题,要注意灵活转化.
的中点共线时,点D到点O距离最大,解决此类问题,要注意灵活转化.
练习册系列答案
相关题目
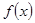 是奇函数,且在区间
是奇函数,且在区间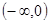 上是单调增函数,又
上是单调增函数,又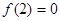 ,则
,则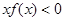 的解集为 .
的解集为 .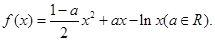
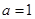 时,求函数
时,求函数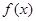 的极值;
的极值;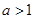 时,讨论函数
时,讨论函数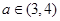 及任意
及任意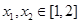 ,恒有
,恒有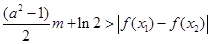 成立,求实数
成立,求实数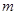 的取值范围.
的取值范围.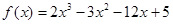 在
在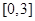 上的最大值和最小值分别是 ( )
上的最大值和最小值分别是 ( ) 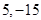
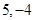
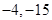
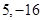
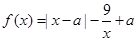 ,
,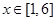 ,
,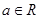 .
. ,试判断并证明函数
,试判断并证明函数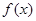 的单调性;
的单调性;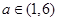 时,求函数
时,求函数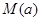 .
.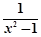 在区间(1,+∞)上的单调性,并用单调性定义证明.
在区间(1,+∞)上的单调性,并用单调性定义证明.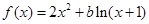 ,其中
,其中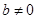 .
.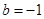 时,求在曲线
时,求在曲线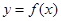 上一点
上一点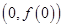 处的切线方程;
处的切线方程;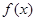 的极值点。
的极值点。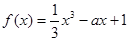 .
.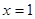 时,
时,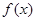 取得极值,求实数
取得极值,求实数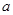 的值;
的值;
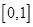 上的最小值;
上的最小值;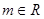 ,直线
,直线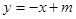 都不是曲线
都不是曲线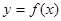 的切线,求实数
的切线,求实数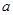 为实数,
为实数,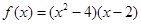 ,
,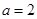 ,求
,求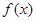 的单调区间;
的单调区间;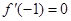 ,求
,求