题目内容
(本题满分14分)定义:对于函数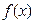 ,
,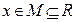 .若
.若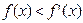 对定义域内的
对定义域内的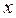 恒成立,则称函数
恒成立,则称函数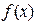 为
为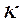 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为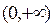 的
的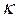 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为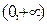 的
的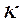 函数
函数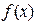 ,求证:对于定义域内的任意正数
,求证:对于定义域内的任意正数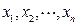 ,均有
,均有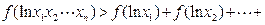
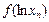 ;
;
(3)对于值域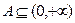 的
的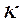 函数
函数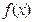 ,求证:
,求证: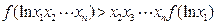 .
.
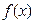 ,
,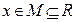 .若
.若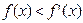 对定义域内的
对定义域内的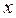 恒成立,则称函数
恒成立,则称函数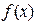 为
为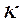 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为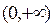 的
的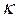 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为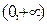 的
的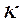 函数
函数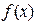 ,求证:对于定义域内的任意正数
,求证:对于定义域内的任意正数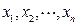 ,均有
,均有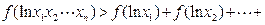
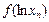 ;
;(3)对于值域
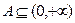 的
的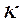 函数
函数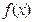 ,求证:
,求证: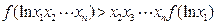 .
.(Ⅰ) (Ⅱ)见解析 (Ⅲ)见解析
(Ⅱ)见解析 (Ⅲ)见解析
 (Ⅱ)见解析 (Ⅲ)见解析
(Ⅱ)见解析 (Ⅲ)见解析(1)如函数 就是定义域内的
就是定义域内的 函数.
函数.
下面进行证明: 必定成立.
必定成立.
(2)构造函数 ,
, ,
,
即 在R上递增所以
在R上递增所以 ,
,
 ,…
,…
得到 ,
, ,
,
…
相加后,得到:
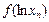
(3)构造函数 ,则
,则 ,因为
,因为 ,所以
,所以


得到 有
有
所以 ,…,
,…,
所以有
 就是定义域内的
就是定义域内的 函数.
函数.下面进行证明:
 必定成立.
必定成立.(2)构造函数
 ,
, ,
,即
 在R上递增所以
在R上递增所以 ,
, ,…
,…
得到
 ,
, ,
,…

相加后,得到:

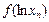
(3)构造函数
 ,则
,则 ,因为
,因为 ,所以
,所以


得到
 有
有
所以
 ,…,
,…,
所以有


练习册系列答案
相关题目
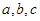 是互不相等的正数,
是互不相等的正数,

 ,
, ,
, 均为正数,且
均为正数,且 +
+ +
+


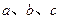 均为正实数,满足关系式
均为正实数,满足关系式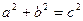 ,又
,又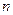 为不小于
为不小于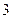 的自然数,求证:
的自然数,求证: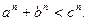
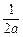 +
+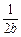 +
+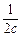 ≥
≥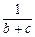 +
+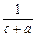 +
+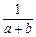 .
. 若
若 且
且 ,求证:
,求证: 或
或 中至少有一个成立.
中至少有一个成立. ≥9;
≥9; ≥
≥ .
.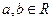 ,求证:
,求证: