题目内容
在数列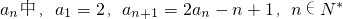
(I)证明数列{an-n}是等比数列;
(II)设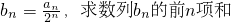 Sn.
Sn.
解:(I)由题设an+1=2an-n+1,可得an+1-(n+1)=2(an-n),
又a1-1=1,所以数列{an-n}首项为1,公比为2的等比数列;
(II)由(I)可知an-n=2n-1,于是数列{an}的通项公式为an=2n-1+n,
所以数列bn= =
=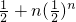 ,
,
所以Sn= +[1
+[1 +2
+2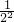 +3•
+3• +…+(n-1)
+…+(n-1)
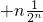 ],
],
设Tn=1 +2
+2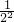 +3•
+3• +…+(n-1)
+…+(n-1)
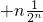 ①
①
所以 Tn=1
Tn=1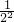 +2
+2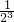 +3•
+3• +…+(n-1)
+…+(n-1)
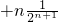 ②
②
①-②可得 Tn=
Tn= +
+ +
+
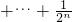
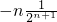
=
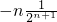 =1-
=1-
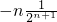 =1
=1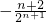 ,
,
故Tn=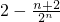 ,故Sn=
,故Sn= +
+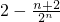 =
=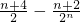
分析:(I)变形原条件可得an+1-(n+1)=2(an-n),易确定等比关系;(II)由(I)可得{an}的通项公式,进而可得{bn}的通项公式,由错位相减法易得答案.
点评:本题考查等比关系的确定和错位相减法求和,属中档题.
又a1-1=1,所以数列{an-n}首项为1,公比为2的等比数列;
(II)由(I)可知an-n=2n-1,于是数列{an}的通项公式为an=2n-1+n,
所以数列bn=
 =
=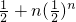 ,
,所以Sn=
 +[1
+[1 +2
+2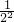 +3•
+3• +…+(n-1)
+…+(n-1)
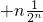 ],
],设Tn=1
 +2
+2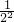 +3•
+3• +…+(n-1)
+…+(n-1)
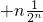 ①
①所以
 Tn=1
Tn=1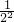 +2
+2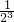 +3•
+3• +…+(n-1)
+…+(n-1)
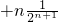 ②
②①-②可得
 Tn=
Tn= +
+ +
+
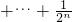
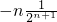
=

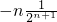 =1-
=1-
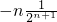 =1
=1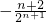 ,
,故Tn=
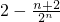 ,故Sn=
,故Sn= +
+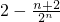 =
=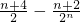
分析:(I)变形原条件可得an+1-(n+1)=2(an-n),易确定等比关系;(II)由(I)可得{an}的通项公式,进而可得{bn}的通项公式,由错位相减法易得答案.
点评:本题考查等比关系的确定和错位相减法求和,属中档题.

练习册系列答案
相关题目
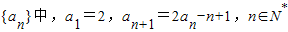
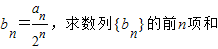 Sn.
Sn.