题目内容

已知函数在（﹣∞，+∞）上是增函数，则m的取值范围是（　　）

　

A．

m＜﹣4或m＞﹣2

B．

﹣4＜m＜﹣2

C．

2＜m＜4

D．

m＜2或m＞4

解答：

解：

对求导，得

f′（x）=x2﹣2（4m﹣1）x+（15m2﹣2m﹣7）

已知函数在（﹣∞，+∞）上是增函数

故f′（x）＞0

即求使x2﹣2（4m﹣1）x+（15m2﹣2m﹣7）＞0的m的取值范围

可以看出函数开口向上，使△＜0即可

对[﹣2（4m﹣1）]2﹣4（15m2﹣2m﹣7）＜0求解，得

2＜m＜4

故选C

练习册系列答案
相关题目
已知函数
a
=（2sinx，2cos2x-1），
b
=（
3
cosx，1），f（x）=
a
•b
（x∈R），
b
=（
3
cosx，1），f（x）=
a
•
b
 （x∈R）
（1）求函数f（x）的最小正周期及在区间[0，
π
2
]上的最大值和最小值；
（2）若f（x0）=
6
5
，x0∈[
π
4
，
π
2
]，求cos2x0的值．
已知函数f（x）=2
3
sinxcosx+2cos2x-1(x∈R)．
（1）求函数f（x）的最小正周期及在[0，
π
2
]上的单调递增区间；
（2）若f（x0）=
6
5
，x0∈[
π
4
，
π
2
]，求cos2x0的值．
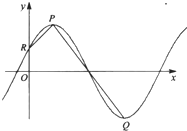（2013•汕头一模）已知函数．f（x）=Asin（
π
3
x+φ），x∈R，A＞0，0＜φ＜
π
2
，y=f（x）的部分图象如图所示，点R（0，
A
2
）是该图象上的一点，P，Q分别为该图象在y轴右侧的第一个最高点和第一个最低点，且 
PR
•
PQ
=1．
（1）求φ和A的值；
（2）若f（
3α
π
）=
6
5
，求cos（2α+
π
3
）的値．
已知函数f(x)=(1+
1
tanx
)sin2x+msin(x+
π
4
)sin(x-
π
4
)．
（1）当m=0时，求函数f（x）在区间(
π
8
，
3π
4
)上的取值范围；
（2）当tanα=2时，f(α)=
6
5
，求m的值．
已知函数f（x）=（a+
1
a
）lnx+
1
x
-x（a＞1）
（1）讨论函数f（x）在（0，1）上的单调性；
（2）a当≥3时，曲线y=f（x）上总存在相异两点，P（x1，f（x1）），Q（x2，f（x2））使得y=f（x）曲线在P、Q处的切线互相平行，求证：x1+x2＞
6
5
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网