题目内容
设函数
，对任意x∈[1，+∞），f（2mx）+2mf（x）＜0恒成立，则实数 m的取值范围是
- A.
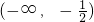
- B.
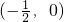
- C.
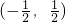
- D.
A
分析：根据函数解析式，整理可得
＜0，分类讨论，转化为解m的不等式，即可求得结论．
解答：∵函数，f（2mx）+2mf（x）＜0
∴＜0
①m＞0，x≥1，∴8m2x2-（1+4m2）＜0，∴
∵x≥1，∴对一切x≥1，不可能始终满足条件；
②m＜0，x≥1，∴8m2x2-（1+4m2）＞0，∴
∵x≥1，∴
，∴m＜-
或m＞
∵m＜0，∴m＜-
故选A．
点评：本题考查恒成立问题，考查分类讨论的数学思想，考查学生分析解决问题的能力，属于中档题．
分析：根据函数解析式，整理可得
＜0，分类讨论，转化为解m的不等式，即可求得结论．解答：∵函数
，f（2mx）+2mf（x）＜0∴
＜0①m＞0，x≥1，∴8m2x2-（1+4m2）＜0，∴
∵x≥1，∴对一切x≥1，不可能始终满足条件；
②m＜0，x≥1，∴8m2x2-（1+4m2）＞0，∴
∵x≥1，∴
，∴m＜-或m＞∵m＜0，∴m＜-
故选A．
点评：本题考查恒成立问题，考查分类讨论的数学思想，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
，对任意x∈[1，+∞），f（2mx）+2mf（x）＜0恒成立，则实数 m的取值范围是（ ）
，对任意x∈[1，+∞），f（2mx）+2mf（x）＜0恒成立，则实数 m的取值范围是（ ）
，对任意x∈[1，+∞），f（mx）+mf（x）＜0恒成立，则实数m的取值范围是（ ）
，对任意x∈[1，+∞），f（mx）+mf（x）＜0恒成立，则实数m的取值范围是（ ）
，对任意x∈[1，+∞），f（mx）+mf（x）＜0恒成立，则实数m的取值范围是（ ）