Question

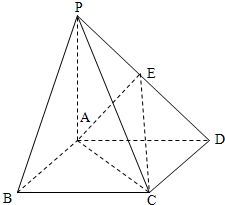
如图，正方体ABCD-A₁B₁C₁D₁的棱长为4，E，F分别是BC，CD上的点，且BE=CF=3．
（1）求B₁F与平面BCC₁B₁所成角的正切值；
（2）求证：B₁F⊥D₁E．

Answer 1

（1）在正方体ABCD-A₁B₁C₁D₁中，CD⊥平面BCC₁B₁，
连接B₁C，则∠FB₁C为B₁F与平面BCC₁B₁所成的角，…（4分）
又∠B₁CF=90°，CF=3，B1C=4

2

，
所以tan∠FB1C=

CF

B1C

=

3 2

8

、…（6分）
（2）如图，以D为坐标原点，直线DA、DC、DD₁分别x轴、y轴、z轴，建立空间直角坐标系．
则D₁（0，0，4），E（1，4，0），F（0，1，0），B₁（4，4，4），

D1E

=(1，4，-4)，

B1F

=(-4，-3，-4)，…（11分）
计算得

D1E

•

B1F

=0，所以B₁F⊥D₁E．…（12分）