题目内容
在△ABC中，
，设x
=0(x，y∈R)，则x-y=_______.
答案：1 【解析】本题考查平面向量的线性运算.据已知可得：
x
=x=(x-1-y)
+(1-
)
=0,
由于向量
、
不共线可作为平面向量的一组基底,
故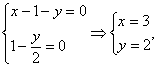
故x-y=1.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，设x=0(x，y∈R)，则x-y=_______.天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
在△ABC中，，设x=0(x，y∈R)，则x-y=_______.
答案：1 【解析】本题考查平面向量的线性运算.据已知可得：
x
=x=(x-1-y)+(1-)=0,
由于向量、不共线可作为平面向量的一组基底,
故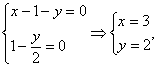故x-y=1.
天天向上一本好卷系列答案小学生10分钟应用题系列答案
在△ABC中，已知P为中线AD的中点．过点P作一直线分别和边AB、AC交于点M、N，设