题目内容
在三棱锥S—ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=4,SB=4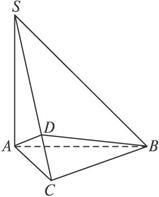
(1)证明SC⊥BC;
(2)求二面角A-BC-S的大小;
(3)求直线AB与平面SBC所成角的大小.(用反三角函数表示)
解法一:(1)证明:∵SA⊥AB,SA⊥AC,且AB∩AC=A,∴SA⊥平面ABC.
∴AC为SC在平面ABC内的射影.
又AC⊥BC,∴BC⊥SC.
(2)由(1)BC⊥SC,又BC⊥AC,∴∠SCA为所求二面角的平面角.
又∵SB=4![]() ,BC=4,
,BC=4,
∴SC=4.∵AC=2,∴∠SCA=60°,
即二面角ABCS的大小为60°.

(3)过A作AD⊥SC于D,连结BD,由(2)得BC⊥平面SAC,又BC![]() 平面SBC,∴平面SAC⊥平面SBC,且平面SAC∩平面SBC=SC.
平面SBC,∴平面SAC⊥平面SBC,且平面SAC∩平面SBC=SC.
∴AD⊥平面SBC.
∴BD为AB在平面SBC内的射影.
∴∠ABD为AB与平面SBC所成角.
在Rt△ABC中,AB=2![]() ,在Rt△SAC中,SA=
,在Rt△SAC中,SA=![]() =2
=2![]() ,
,
AD=![]() ,∴sin∠ABD=
,∴sin∠ABD=![]() =
=![]() .
.
∴直线AB与平面SBC所成角的大小为arcsin![]() .
.
解法二:(1)证明:由已知∠SAB=∠SAC=∠ACB=90°,
以C点为原点,建立如图所示的空间直角坐标系C—xyz.
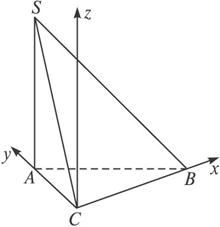
则A(0,2,0),B(4,0,0),C(0,0,0),S(0,2,2![]() ).
).
则![]() =(0,-2,-2
=(0,-2,-2![]() ),
),![]() =(-4,0,0).∴
=(-4,0,0).∴![]() ·
·![]() =0.∴SC⊥BC.
=0.∴SC⊥BC.
(2)∵∠SAB=∠SAC=90°,∴SA⊥平面ABC.
∴![]() =(0,0,2
=(0,0,2![]() )是平面ABC的法向量.
)是平面ABC的法向量.
设侧面SBC的法向量为n=(x,y,z),![]() =(0,-2,-2
=(0,-2,-2![]() ),
),![]() =(-4,0,0).
=(-4,0,0).
∵![]() ·n=0,
·n=0,![]() ·n=0,∴
·n=0,∴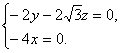 ∴x=0.令z=1,则y=-
∴x=0.令z=1,则y=-![]() .
.
则平面SBC的一个法向量n=(0,-![]() ,1).7分cos〈
,1).7分cos〈![]() ,n〉=
,n〉=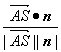 =
=![]() =
=![]() ,
,
即二面角ABCS的大小为60°.
(3)由(2)可知n=(0,![]() ,1)是平面SBC的一个法向量.
,1)是平面SBC的一个法向量.
又![]() =(4,-2,0),∴cos〈
=(4,-2,0),∴cos〈![]() ,n〉=
,n〉=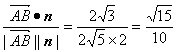 .
.
∴直线AB与平面SBC所成角为arcsin![]() .
.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.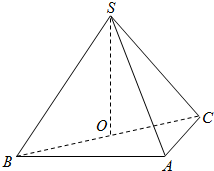 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. 如图,在三棱锥S-ABC中,
如图,在三棱锥S-ABC中,