题目内容
16.在平面直角坐标系xOy中,圆C的方程为(x-2)2+y2=1,点P在直线l:x+y+1=0上,若过点P存在直线m与圆C交于A,B两点,且点A为PB中点,则点P的恒坐标的取值范围是[-1,2].分析 设点P(x0,-x0-1),B(2+cosθ,sinθ),求出A的坐标,代入圆C:(x-2)2+y2=1,利用辅助角公式,即可确定点P横坐标x0的取值范围.
解答 解:设点P(x0,-x0-1),B(2+cosθ,sinθ),则
由条件得A点坐标为x=$\frac{1}{2}$(x0+2+cosθ),y=$\frac{1}{2}$(sinθ-x0-1),
从而[$\frac{1}{2}$(x0+2+cosθ)-2]2+[$\frac{1}{2}$(sinθ-x0-1)]2=1,
整理得(x0-2)cosθ-(x0+1)sinθ+x02-x0+1=0,
从而$\sqrt{2{{x}_{0}}^{2}-2{x}_{0}+5}$sin(θ+α)=-x02+x0-1,
于是由$\sqrt{2{{x}_{0}}^{2}-2{x}_{0}+5}$≥|-x02+x0-1|,解得-1≤x0≤2.
故答案为:[-1,2].
点评 本题考查直线与圆的位置关系,考查参数法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
11.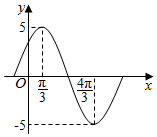 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=3,α∈($\frac{π}{3}$,$\frac{5π}{6}$),则sinα的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=3,α∈($\frac{π}{3}$,$\frac{5π}{6}$),则sinα的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=3,α∈($\frac{π}{3}$,$\frac{5π}{6}$),则sinα的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,若f(α)=3,α∈($\frac{π}{3}$,$\frac{5π}{6}$),则sinα的值为( )| A. | $\frac{3\sqrt{3}+4}{10}$ | B. | $\frac{3\sqrt{3}-4}{10}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |
6.设二项式(x-y)m(m∈N*)的展开式中,x4yr的系数为-35,则(2x+$\frac{1}{2\sqrt{x}}$)r+3的展开式中,常数项为( )
| A. | $\frac{21}{2}$ | B. | $\frac{15}{4}$ | C. | 10 | D. | 5 |
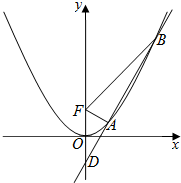 已知抛物线C:x2=4y的焦点为F,过点D(0,-1)的直线l与抛物线C交于不同的A、B两点.
已知抛物线C:x2=4y的焦点为F,过点D(0,-1)的直线l与抛物线C交于不同的A、B两点.