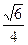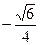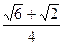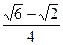题目内容
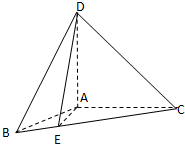
如图,用一副直角三角板拼成一直二面角A-BD-C,若其中给定AB=AD=2,∠BCD=90°,∠BDC=60°,
(Ⅰ)求三棱锥A-BCD的体积;
(Ⅱ)求点A到BC的距离.
(Ⅰ)求三棱锥A-BCD的体积;
(Ⅱ)求点A到BC的距离.

(Ⅰ)∵直二面角A-BD-C是由一付直角三角板拼成
又∵AB=AD=2,则△ABD是以A为直角的等腰直角三角形,BD=2
又∵∠BCD=90°,∠BDC=60°,
∴CD=
,BC=
,S△BCD=
•
•
=
取BD的中点E,连接AE,则AE⊥BD,AE=
,如图所示
则AE⊥平面BCD,
则VA-BCD=
•AE•S△BCD=
•
•
=
(Ⅱ)过E点做EF∥CD,则EF=
,且EF⊥BC
又∵AE⊥BC,AE∩EF=E
则BC⊥平面AEF
∴AF⊥BC,则线段AF长即为A点到BC的距离
在直角三角形AEF中,AF=
=
=
=

又∵AB=AD=2,则△ABD是以A为直角的等腰直角三角形,BD=2
| 2 |
又∵∠BCD=90°,∠BDC=60°,
∴CD=
| 2 |
| 6 |
| 1 |
| 2 |
| 2 |
| 6 |
| 3 |
取BD的中点E,连接AE,则AE⊥BD,AE=
| 2 |
则AE⊥平面BCD,
则VA-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| ||
| 3 |
(Ⅱ)过E点做EF∥CD,则EF=
| ||
| 2 |
又∵AE⊥BC,AE∩EF=E
则BC⊥平面AEF
∴AF⊥BC,则线段AF长即为A点到BC的距离
在直角三角形AEF中,AF=
| AE2+EF2 |
2+
|
|
| ||
| 2 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
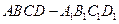 中,
中,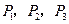 分别是棱
分别是棱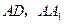 及
及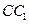 的中点,试作出经过
的中点,试作出经过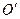 为其圆心)上,且点A、C、D、
为其圆心)上,且点A、C、D、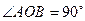 ,则异面直线AB与CD所成角的余弦值为 ( )
,则异面直线AB与CD所成角的余弦值为 ( )