题目内容
已知定义域为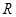 的函数
的函数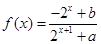 是奇函数.
是奇函数.
(1)求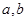 的值;
的值;
(2)判断函数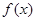 的单调性,并证明.
的单调性,并证明.
【答案】
(1)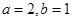 ;(2)减函数,证明详见解析;
;(2)减函数,证明详见解析;
【解析】
试题分析:(1)因为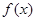 是奇函数,且定义域为
是奇函数,且定义域为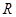 ,可由
,可由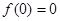 和
和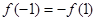 列式求出
列式求出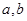 的值,但要注意
的值,但要注意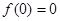 和
和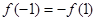 只是本题中的
只是本题中的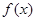 是奇函数的必要条件,然后还要验证充分性;(2)判断函数的单调性在解答题中一般利用增函数或减函数的定义,或利用导函数的符号判断.
是奇函数的必要条件,然后还要验证充分性;(2)判断函数的单调性在解答题中一般利用增函数或减函数的定义,或利用导函数的符号判断.
试题解析:(1)因为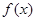 是奇函数,且定义域为
是奇函数,且定义域为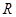 ,所以
,所以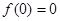 , 2分
, 2分
所以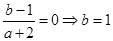 ,所以
,所以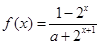 4分
4分
又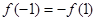 ,知
,知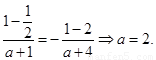
经验证,当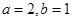 时,
时,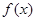 是奇函数,所以
是奇函数,所以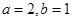 7分
7分
(2)函数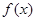 在
在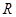 上为减函数
9分
上为减函数
9分
证明:法一:由(1)知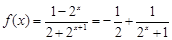 ,
,
令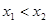 ,则
,则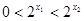 ,
,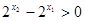 12分
12分
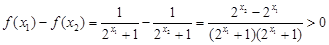 ,
,
即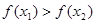 ,
, 函数
函数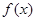 在
在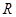 上为减函数
14分
上为减函数
14分
法二:由(1)知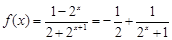 ,
,
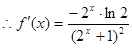 ,
12分
,
12分
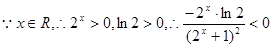 ,
,
即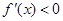
 函数
函数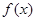 在
在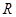 上为减函数.
14分
上为减函数.
14分
考点:函数的奇偶性、函数的单调性.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
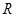 的函数
的函数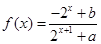 是奇函数。
是奇函数。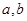 的值;
的值;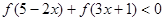
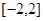 的函数
的函数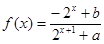 是奇函数.
是奇函数.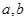 的值; (Ⅱ)解关于
的值; (Ⅱ)解关于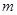 的不等式
的不等式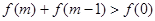 .
.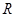 的函数
的函数 是奇函数.
是奇函数. 的值;
的值;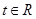 ,不等式
,不等式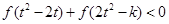 恒成立,求
恒成立,求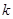 的取值范围.
的取值范围.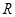 的函数
的函数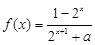 是奇函数.
是奇函数.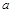 的值;
的值;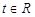 ,不等式
,不等式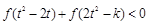 恒成立,求实数
恒成立,求实数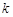 的取值范围.
的取值范围. 的函数
的函数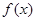 是偶函数,当
是偶函数,当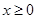 时,
时,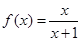 .
.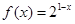 在区间
在区间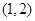 上有解
上有解