题目内容
（本小题满分12分）
已知定义域为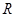
的函数
是奇函数．
（1）求
的值；
（2）若对任意的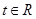
，不等式
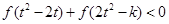恒成立，求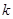
的取值范围.
【答案】
（1）
（2）
【解析】
试题分析:（1）因为
是奇函数，所以
，即
……2分
又由
知
综上所述，
……4分
（2）由（1）知
，
易知在
上为减函数．
……6分
又因是奇函数，从而有不等式：
等价于
，……8分
因为减函数，由上式推得：
．
即对一切
有：
，
从而判别式
……12分
考点：本小题考查函数的奇偶性、单调性及恒成立问题.
点评：函数的奇偶性、单调性及恒成立问题，都是高考中常考的内容.解决恒成立问题一般都转化成求最值来解决，而要求函数的最值，函数的单调性是高考中一定会考查的内容.
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
