题目内容
已知数列{an},Sn是其前n项和,且an=7Sn-1+2(n≥2),a1=2.
(1)求数列{an} 的通项公式;
(2)设bn=
,Tn是数列 {bn}的前n项和,求T10的值.
(1)求数列{an} 的通项公式;
(2)设bn=
| 1 |
| log2an•log2an+1 |
(1)∵n≥2时,an=7Sn-1+2,∴an+1=7Sn+2,an+1-an=7an,
∴an+1=8an,(n≥2)
又a1=2.∴a2=16=8a1.
an+1=8an,(n≥N*)
∴数列{an}是一个以2为首项,8为公比的等比数列
∴数列an=23n-2
(2)bn=
=
=
(
-
)
∴Tn=
(1-
+
-
+…+
-
)=
(1-
)∴T10=
∴an+1=8an,(n≥2)
又a1=2.∴a2=16=8a1.
an+1=8an,(n≥N*)
∴数列{an}是一个以2为首项,8为公比的等比数列
∴数列an=23n-2
(2)bn=
| 1 |
| log2an•log2an+1 |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
∴Tn=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 3n+1 |
| 10 |
| 31 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
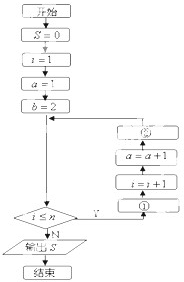 已知数列{an}的通项公式为an=n•2n,为了求数列{an}的和,现已给出该问题的算法程序框图.
已知数列{an}的通项公式为an=n•2n,为了求数列{an}的和,现已给出该问题的算法程序框图.