题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 与
与![]() 在公共点
在公共点![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)当![]() 时,若曲线
时,若曲线![]() 与
与![]() 在公共点
在公共点![]() 处有相同的切线,求证:点
处有相同的切线,求证:点![]() 唯一;
唯一;
(3)若![]() ,
, ![]() ,且曲线
,且曲线![]() 与
与![]() 总存在公切线,求:正实数
总存在公切线,求:正实数![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)证明见解析;(3)1.
;(2)证明见解析;(3)1.
【解析】试题分析:(1)![]() 曲线
曲线![]() 与
与![]() 在公共点
在公共点![]() 处有相同的切线,
处有相同的切线, 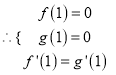 ,解出即可;(2)设
,解出即可;(2)设![]() ,由题设得
,由题设得![]() ,转化为关于
,转化为关于![]() 的方程只有一解,进而构造函数转化为函数只有一个零点,利用导数即可证明;(3)设曲线
的方程只有一解,进而构造函数转化为函数只有一个零点,利用导数即可证明;(3)设曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,则只需使该切线与
,则只需使该切线与![]() 相切即可,也即方程组
相切即可,也即方程组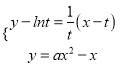 ,只有一解即可,所以消去
,只有一解即可,所以消去![]() 后
后![]() ,问题转化关于
,问题转化关于![]() 方程总有解,分情况借助导数进行讨论即可求得
方程总有解,分情况借助导数进行讨论即可求得![]() 值.
值.
试题解析:(1)![]() ,
,![]() .∵曲线
.∵曲线![]() 与
与![]() 在公共点
在公共点![]() 处有相同的切线∴
处有相同的切线∴ 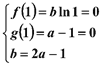 , 解得,
, 解得,![]() .
.
(2)设![]() ,则由题设有
,则由题设有![]() … ①又在点
… ①又在点![]() 有共同的切线
有共同的切线
∴![]() 代入①得
代入①得 ![]()
设![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,所以
上单调递增,所以 ![]() =0最多只有
=0最多只有![]() 个实根,
个实根,
从而,结合(Ⅰ)可知,满足题设的点![]() 只能是
只能是![]()
(3)当![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
由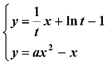 ,得
,得 ![]() .
.
∵ 曲线![]() 与
与![]() 总存在公切线,∴ 关于
总存在公切线,∴ 关于![]()
![]() 的方程
的方程![]() ,
,
即![]()
![]() 总有解.
总有解.
若![]() ,则
,则![]() ,而
,而![]() ,显然
,显然![]() 不成立,所以
不成立,所以 ![]() .
.
从而,方程![]() 可化为
可化为 ![]() .
.
令![]()
![]() ,则
,则![]() .
.
∴ 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,即
,即 ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.∴
上单调递增.∴![]() 在
在![]() 的最小值为
的最小值为![]() ,
,
所以,要使方程![]() 有解,只须
有解,只须![]() ,即
,即![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目