题目内容
【题目】已知椭圆C中心在原点,焦点在坐标轴上,且该椭圆经过点( ![]() ,
, ![]() )和点
)和点 ![]() .求
.求
(1)椭圆C的方程;
(2)P,Q,M,N四点在椭圆C上,F1为负半轴上的焦点,直线PQ,MN都过F1且 ![]() ,求四边形PMQN的面积最小值和最大值.
,求四边形PMQN的面积最小值和最大值.
【答案】
(1)解:由题意,设椭圆的方程为mx2+ny2=1(m,n>0,m≠n),
代入点( ![]() ,
, ![]() )和点
)和点 ![]() ,可得
,可得
![]() m+
m+ ![]() n=1,
n=1, ![]() m+n=1,
m+n=1,
解得m=1,n= ![]() ,
,
即有椭圆方程为x2+ ![]() =1
=1
(2)解:由 ![]() ,可得直线PQ,MN垂直.
,可得直线PQ,MN垂直.
(ⅰ)若MN与PQ中一条斜率不存在,另一条斜率为0,
则四边形PMQN的面积S= ![]() 2a
2a ![]() =2b2=2;
=2b2=2;
(ⅱ)若PQ与NM的斜率均存在,
设PQ:y=kx+1与椭圆方程联立 ![]()
消去y可得(2+k2)x+2kx﹣1=0,则△=8(k2+1)>0,
设P(x1,y1),Q(x2,y2),
则x1+x2=﹣ ![]() ,x1x2=﹣
,x1x2=﹣ ![]() ,
,
∴|PQ|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]() =2
=2 ![]()
![]() ;
;
同理可得|MN|=2 ![]()
![]() .
.
∴S= ![]() |PQ||MN|=4
|PQ||MN|=4 ![]() =
= 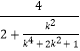 =
= 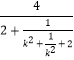 ,
,
由k2+ ![]() ≥2,得
≥2,得 ![]() ≤S<2.
≤S<2.
由(ⅰ)(ⅱ)知,Smin= ![]() ,Smax=2
,Smax=2
【解析】(1)由题意,设椭圆的方程为mx2+ny2=1(m,n>0,m≠n),代入两点的坐标,建立方程组,从而可求椭圆的几何量,即可求椭圆C的方程;(2)分斜率存在与存在分别讨论,利用直线与椭圆联立,根据韦达定理及弦长公式,确定面积的表达式,运用基本不等式可得最值,即可求得结论.

练习册系列答案
相关题目