题目内容
求抛物线y=-3x2+2在点P(1,-1)处的切线方程.
分析：已知切点的坐标,只要求出切线的斜率即可.
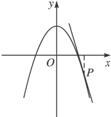
解：抛物线y=-3x2+2在点P(1,-1)处的切线斜率为
k=
=
=
=
(-6-3Δx)=-6.
所以,切线方程为y-(-1)=-6(x-1),即6x+y-5=0.
练习册系列答案
相关题目
题目内容
求抛物线y=-3x2+2在点P(1,-1)处的切线方程.
分析：已知切点的坐标,只要求出切线的斜率即可.
解：抛物线y=-3x2+2在点P(1,-1)处的切线斜率为
k=
=
=
=(-6-3Δx)=-6.
所以,切线方程为y-(-1)=-6(x-1),即6x+y-5=0.
设f（x）为定义在R上的偶函数，当0≤x≤2时，y=
