题目内容
设数列{an}、{bn}、{cn}满足：bn＝an－an＋2，cn＝an＋2an＋1＋3an＋2(n＝1，2，3，…)，求证：{an}为等差数列的充分必要条件是{cn}为等差数列且bn≤bn＋1(n＝1，2，3，…)．
证明：必要性：
设{an}是公差为d1的等差数列，则
bn＋1－bn＝(an＋1－an＋3) － (an－an＋2)
＝ (an＋1－an) － (an＋3－an＋2)＝ d1－ d1＝0，
所以bn≤bn＋1(n＝1，2，3，…)成立．
又cn＋1－cn＝(an＋1－an)＋2(an＋2－an＋1)＋3(an＋3－an＋2)＝ d1＋2d1 ＋3d1 ＝6d1(常数)(n＝1，2，3，…)，
所以数列{cn}为等差数列．
充分性：
设数列{cn}是公差为d2的等差数列，且bn≤bn＋1(n＝1，2，3，…)．
∵ cn＝an＋2an＋1＋3an＋2， ①
∴ cn＋2＝an＋2＋2an＋3＋3an＋4， ②
①－②，得cn－cn＋2＝(an－an＋2)＋2 (an＋1－an＋3)＋3 (an＋2－an＋4)＝bn＋2bn＋1＋3bn＋2.
∵ cn－cn＋2＝(cn－cn＋1)＋(cn＋1－cn＋2)＝ －2d2，
∴ bn＋2bn＋1＋3bn＋2＝－2d2， ③
从而有bn＋1＋2bn＋2＋3bn＋3＝－2d2， ④
④－③，得(bn＋1－bn)＋2 (bn＋2－bn＋1)＋3 (bn＋3－bn＋2)＝0.⑤
∵ bn＋1－bn≥0，bn＋2－bn＋1≥0，bn＋3－bn＋2≥0，
∴ 由⑤得bn＋1－bn＝0(n＝1，2，3，…)．
由此不妨设bn＝d3 (n＝1，2，3，…)，则an－an＋2＝d3(常数)．
由此cn＝an＋2an＋1＋3an＋2cn＝4an＋2an＋1－3d3，
从而cn＋1＝4an＋1＋2an＋2－5d3，
两式相减得cn＋1－cn＝2(an＋1－an) －2d3，
因此an＋1－an＝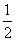
(cn＋1－cn)＋d3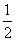＝d2＋d3(常数) (n＝1，2，3，…)，
∴ 数列{an}为等差数列．
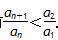
的概率为( )
B.
D.
表示的平面区域内存在点P(x0，y0)，满足x0－2y0＝2.求得m的取值范围是( )