Question

如图，已知三棱锥P—ABC中，PA=PC，∠APC=∠ACB=90°,∠BAC=30°,平面PAC⊥平面ABC.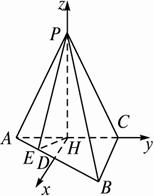

(1)求证：平面PAB⊥平面PBC；

（2）求二面角P—AB—C的大小.

Answer 1

（1）证明：∵PA=PC,面PAC⊥面ABC，∠ACB=90°,取AC的中点H，则PH⊥底面ABC，取AB的中点D，以H为原点，HD、HC、HP分别为x轴、y轴、z轴建立直角坐标系.如图所示，设PA=PC=2a，则?

P（0，0，a），C（0，a，0），A（0，-a，0），D（a，0，0），B（,a,0）.

=(0,a,a),=(0,a,-a),?

=(-a,0,0).?

则=0，=0，?

∴AP⊥PC,AP⊥BC,∴AP⊥面PBC，?

∴面PAB⊥面PBC.

(2)解：连结PD，过P作PE⊥AB于E，连接EH，则∠PEH即为二面角P—AB—C的平面角，可得E点的坐标为(a,-a,0),cos∠PEH==.∴∠PEH=arccos.?

即二面角PABC的平面角为arccos.