Question

如图，已知三棱锥P-ABC中，PA⊥平面ABC，AN⊥BC于N，D是AB的中点，且PA=1，AN=BN=CN=

2

．
（1）求证：PB⊥AC；
（2）求异面直线CD与PB所成角的大小；
（3）求点A到平面PBC的距离．

Answer 1

分析：（1）根据线面垂直的判定定理可知，只需证直线与平面中的两条相交直线垂直即可；
（2）先通过平移将两条异面直线平移到同一个起点D，得到的锐角或直角就是异面直线所成的角，在三角形中再利用余弦定理求出此角即可；
（3）先在图形中找出面PBC的垂线，再在直角三角形中求垂距离即可．

解答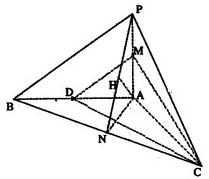：解：（1）∵AN⊥BC，且AN=BN=CN=

2

，
∴AB=AC且AB⊥AC．（2分）
∵PA⊥平面ABC，
∴AB是PB在平面ABC内的射影．
∵PB⊥AC．（5分）

（2）取PA的中点M，连接DM，CM，则DM∥PB．
∴∠CDM是异面直线CD与PB所成的角．（7分）
由（1）可求得AB=AC=2，
在△CDM中，
DM=

1

2

AB=

5

2

，
CD=

AC2+AD2

=

5

．
CM=

AC2+AM2

=

17

2

．cosCDM=

CD2+DM2-CM2

2CD•DM

=

2

5

．
所以异面直线CD与PB所成角的大小为arccos

2

5

．（9分）

（3）连接PN．
∵PA⊥平面ABC，
又由已知可得CN⊥平面PAN，
∴平面PAN⊥平面ABC．
过A点作AH⊥PN于H，
则AH⊥平面PBC．
∴AH的长就是点A到平面PBC的距离．（11分）
由已知可得BC=2

2

．
∵PA⊥平面ABC．
∴PA⊥AN．
又PN=

PA2+AN2

=

3

，
在Rt△PAN中，
有AH=

PA•AN

PN

=

2

3

=

6

3

．
即点A到平面PBC的距离是

6

3

．（14分）

点评：本小题主要考查异面直线所成的角，以及点、线、面间的距离计算，考查空间想象能力、运算能力和推理论证能力，属于基础题．