题目内容
设f(x)定义域为D,若满足(1)f(x)在D内是单调函数(2)存在[a,b]⊆D使f(x)在x∈[a,b]值域为[a,b],则称f(x)为D上的闭函数.当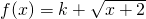 为闭函数时,k的范围是________.
为闭函数时,k的范围是________.
解:∵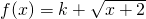 在定义域D=[-2,+∞)上为增函数
在定义域D=[-2,+∞)上为增函数
故满足条件(1)
若存在[a,b]⊆D使f(x)在x∈[a,b]值域为[a,b],
则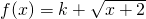 =x在区间[-2,+∞)上有两个根
=x在区间[-2,+∞)上有两个根
令t=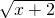 (t≥0)
(t≥0)
则原方程可化为t2-t-(2+k)=0有两个非负根
即
解得- <k≤-2
<k≤-2
故k的范围是
故答案为:
分析:由已知中闭函数的定义,及函数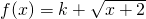 的解析式,我们可得函数满足条件(1),即在定义域D内是单调函数,若满足条件(2)则
的解析式,我们可得函数满足条件(1),即在定义域D内是单调函数,若满足条件(2)则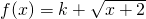 =x在区间[-2,+∞)上有两个根,利用换元法,可将条件转化为t2-t-(2+k)=0有两个非负根,结合二次方程根与系数的关系,可得关于k的不等式组,进而求出k的范围.
=x在区间[-2,+∞)上有两个根,利用换元法,可将条件转化为t2-t-(2+k)=0有两个非负根,结合二次方程根与系数的关系,可得关于k的不等式组,进而求出k的范围.
点评:本题考查的知识点是单调性的性质,其中正确理解新定义“闭函数”中的两个条件的意义,是解答本题的关键.
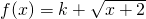 在定义域D=[-2,+∞)上为增函数
在定义域D=[-2,+∞)上为增函数故满足条件(1)
若存在[a,b]⊆D使f(x)在x∈[a,b]值域为[a,b],
则
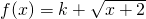 =x在区间[-2,+∞)上有两个根
=x在区间[-2,+∞)上有两个根令t=
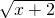 (t≥0)
(t≥0)则原方程可化为t2-t-(2+k)=0有两个非负根
即

解得-
 <k≤-2
<k≤-2故k的范围是

故答案为:

分析:由已知中闭函数的定义,及函数
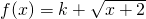 的解析式,我们可得函数满足条件(1),即在定义域D内是单调函数,若满足条件(2)则
的解析式,我们可得函数满足条件(1),即在定义域D内是单调函数,若满足条件(2)则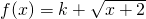 =x在区间[-2,+∞)上有两个根,利用换元法,可将条件转化为t2-t-(2+k)=0有两个非负根,结合二次方程根与系数的关系,可得关于k的不等式组,进而求出k的范围.
=x在区间[-2,+∞)上有两个根,利用换元法,可将条件转化为t2-t-(2+k)=0有两个非负根,结合二次方程根与系数的关系,可得关于k的不等式组,进而求出k的范围.点评:本题考查的知识点是单调性的性质,其中正确理解新定义“闭函数”中的两个条件的意义,是解答本题的关键.

练习册系列答案
相关题目
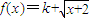 为闭函数时,k的范围是 .
为闭函数时,k的范围是 .