题目内容
已知函数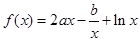 .
.
(I)若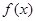 在
在 处取得极值,
处取得极值,
①求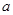 、
、 的值;②存在
的值;②存在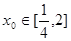 ,使得不等式
,使得不等式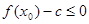 成立,求
成立,求 的最小值;
的最小值;
(II)当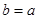 时,若
时,若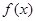 在
在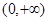 上是单调函数,求
上是单调函数,求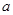 的取值范围.(参考数据
的取值范围.(参考数据 )
)
【答案】
(1)①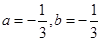 ,②
,②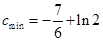 ;(2)
;(2)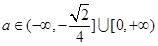
【解析】
试题分析:(1)①根据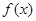 在
在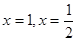 处取得极值,求导将
处取得极值,求导将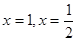 带入到导函数中,联立方程组求出
带入到导函数中,联立方程组求出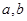 的值;②存在性恒成立问题,
的值;②存在性恒成立问题,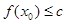 ,只需
,只需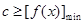 ,进入通过求导求出
,进入通过求导求出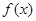 的极值,最值.(2)当
的极值,最值.(2)当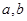 的未知时,要根据
的未知时,要根据 中分子是二次函数形式按
中分子是二次函数形式按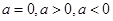 进行讨论.
进行讨论.
试题解析:(1)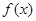 定义域为
定义域为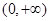 .
.
①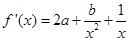 ,
,
因为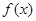 在
在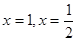 处取和极值,故
处取和极值,故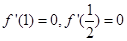 ,
,
即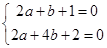 ,解得
,解得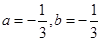 .
.
②由题意:存在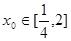 ,使得不等式
,使得不等式 成立,则只需
成立,则只需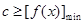
由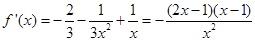 ,令
,令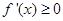 则
则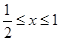 ,令
,令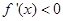 则
则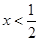 或
或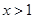 ,
,
所以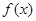 在
在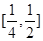 上单调递减,
上单调递减,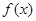 在
在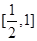 上单调递增,
上单调递增,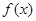 在
在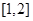 上单调递减
上单调递减
所以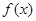 在
在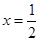 处取得极小值,
处取得极小值,
而最大值需要比较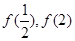 的大小,
的大小,
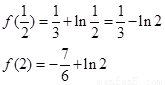 ,
,
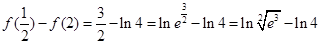 ,
,
比较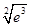 与4的大小,而
与4的大小,而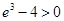 ,所以
,所以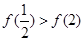
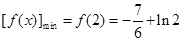
所以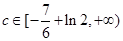
所以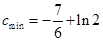 .
.
(2)当
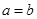 时,
时,
①当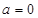 时,
时,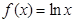 则
则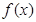 在
在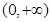 上单调递增;
上单调递增;
②当 时,∵
时,∵
 ,则
,则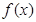 在
在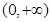 上单调递增;
上单调递增;
③当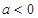 时,设
时,设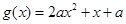 ,只需
,只需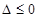 ,从而得
,从而得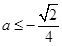 ,此时
,此时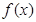 在
在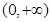 上单调递减;
上单调递减;
综上可得,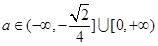 .
.
考点:1.利用导数求函数的极值、最值;2.函数恒成立问题;3.利用单调性求参数范围.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 .
. 的单调区间;
的单调区间; 的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t
的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t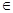 [1,2],函数
[1,2],函数 是
是
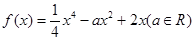 .
.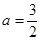 ,求函数
,求函数 极值;ww..com
极值;ww..com
 ,若函数F(x)在[0,1]上单调递增,求
,若函数F(x)在[0,1]上单调递增,求 的取值范围.
的取值范围. .
. 在点
在点 处的切线斜率为4,求实数
处的切线斜率为4,求实数 的值;
的值; 在区间
在区间 上存在零点,求实数
上存在零点,求实数
 ,求
,求 的单调区间;
的单调区间; 在
在 单调增加,在
单调增加,在 单调减少,
单调减少, <6.
<6.